PDO, acrónimo de PHP Data Objects es un interfaz para acceder a bases de datos desde PHP. A diferencia de las extensiones mysql y mysqli, que son exclusivas para MySQL, PDO puede trabajar con diferentes sistemas gestores de bases de datos, siempre y cuando haya driver para el mismo.
Las transacciones sirven para garantizar la integridad referencial de los datos. Una transacción está formada por varias órdenes SQL y bien se ejecutan todas las consultas en bloque o si alguna falla se vuelve al estado inicial antes de empezar la transacción, sin ejecutarse ninguna de ellas. Las transacciones deben cumplir con las propiedades ACID: Atomicidad, Consistencia, Isolation (aislamiento) y Durabilidad. (Nada que ver con el subgénero de música electrónica de finales de los 80 🙂 )
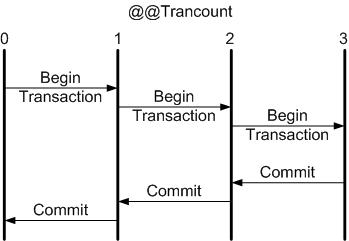
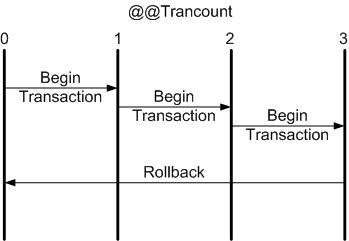
Las transacciones se anidan cuando existiendo una transacción en curso, se inicia otra. Esto por ejemplo sucede cuando desde un método donde se ha iniciado una transacción, para reciclar código (una de las virtudes de la programación orientada a objetos) se llama a otro método que inicia otra transacción.
Todo fue bien hasta el final y se ejecutan en bloque todas las transacciones (COMMIT)
¡Ups, algo fallo cuando ya casi finalizaba! ¡Déjalo todo como estaba! (ROLLBACK)
Desgraciadamente, desarrollando en LAMP, nada más iniciarse la segunda transacción se producirá un error fatal. MySQL no soporta las transacciones anidadas. En su documentación afirma que después de ejecutarse un BEGIN TRANSACTION ciertas órdenes producirán un COMMIT, entre ellas BEGIN TRANSACTION. Tampoco las soporta PostgreSQL. Una solución parcial que ambos sistemas incorporan son los SAVE POINTS.
A continuación viene el esquema de una clase que mediante los SAVE POINTS y controlando el número de transacciones anidadas mediante la propiedad transactionDepth, consigue algo parecido a anidar transacciones y por lo tanto evita el error fatal antes mencionado.
Si tu clase extiende la clase PDO, el método execute puede ser reemplazado llamando simplemente a $this->exec() Como digo, esta clase es un esquema para entender la idea, no está pensada para funcionar directamente sino que el programador interesado en ella deberá adaptarla.
class Db {
static private $instance = null;
private $connection = null;
protected $transactionDepth = 0;
private function __construct() {
}
private function _connect() {
if ($this->connection === null) {
try {
/* Código para conectarse a la BD */
} catch (PDOException $e) {
echo "error pdo: ";
echo $e->getMessage();
}
}
return $this;
}
/* Nada que clonar en el patrón de diseño Singleton */
private function __clone()
{
}
static public function getInstance()
{
if (is_null(self::$instance)) {
self::$instance = new self();
}
return self::$instance;
}
static public function closeConnection()
{
if (!self::$instance === null) {
self::$instance = null;
}
if (isset(self::$connection)) {
unset(self::$connection);
}
}
public function getConnection()
{
$this->_connect();
return $this->connection;
}
protected function prepare($query, $params = array())
{
$stmt = $this->getConnection()->prepare($query);
if (is_array($params)) {
foreach ($params as $param => $value) {
if (is_bool($value)) {
$type = PDO::PARAM_BOOL;
} elseif ($value === null) {
$type = PDO::PARAM_NULL;
} elseif (is_integer($value)) {
$type = PDO::PARAM_INT;
} else {
$type = PDO::PARAM_STR;
}
$stmt->bindValue(":$param", $value, $type);
}
}
return $stmt;
}
public function execute($sql, $params = array())
{
$stmt = $this->prepare($sql, $params);
$stmt->execute();
$stmt->closeCursor();
return $stmt->rowCount();
}
public function begin()
{
if ($this->transactionDepth == 0) {
$this->getConnection()->beginTransaction();
}else{
$this->execute("SAVEPOINT LEVEL{$this->transactionDepth}");
}
$this->transactionDepth++;
}
public function commit()
{
$this->transactionDepth--;
if ($this->transactionDepth == 0) {
return $this->getConnection()->commit();
}else{
return $this->execute("RELEASE SAVEPOINT LEVEL{$this->transactionDepth}");
}
}
public function rollback()
{
if ($this->transactionDepth == 0) {
throw new PDOException("Ninguna transacción en curso para retroceder");
}
$this->transactionDepth--;
if ($this->transactionDepth == 0) {
return $this->getConnection()->rollback();
}else{
return $this->execute("ROLLBACK TO SAVEPOINT LEVEL{$this->transactionDepth}");
}
}
}
El código también está disponible en Github.
