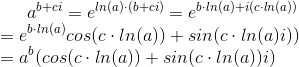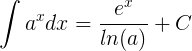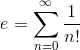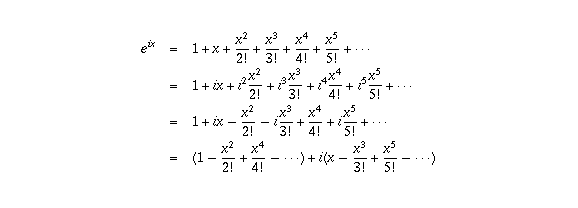Google ha anunciado recientemente que ya no escaneará los emails de los usuarios de Gmail:
Google has decided to follow suit later this year in our free consumer Gmail service. Consumer Gmail content will not be used or scanned for any ads personalization after this change.
Algo que no hacen ni Yahoo ni la compañía más criticada en el pasado reciente por sus prácticas: Microsoft. ¿Qué hubiera pasado si fuera Microsoft la que lee los emails de Hotmail (ahora Outlook)? Probablemente muchos hubieran puesto el grito en el cielo. Pero para Google hay otro rasero.
Cuando hace bastantes años atrás leí que «Don’t be evil» (no seas malvado) es su lema para la conducta interna me llamó la atención leer tantas opiniones favorables a Google, como si fuera fuente de toda virtud. Fui un poco escéptico y pensé que Google, como todas las grandes empresas, tiene como objetivo rendir beneficios a sus accionistas; ni es una ONG ni son las hermanitas de la caridad. El caso es que su estrategia de marketing les funcionó porque durante años todos los usuarios de Gmail hemos estado conformes con que Google escaneé nuestros emails para ofrecernos una publicidad más personalizada. Como bien dice el refrán: más vale caer en gracia que ser gracioso. Google supo desde el principio que no bastaba con tener la mejor tecnología.