En el artículo anterior vimos qué significa y cómo se soluciona la exponenciación de e a un número complejo imaginario puro.
Dejé pendiente cómo se realizaría el cálculo en el caso de que el número complejo del exponente tuviera también parte real, es decir, si no es un imaginario puro. En el presente artículo doy la respuesta, y ésta es muy sencilla pues resulta que e elevado a un número complejo tiene las mismas propiedades que la exponenciación de cualquier otro tipo de números. Dado el número complejo b + ci tenemos que:
En el artículo anterior ya vimos el cálculo de eci. Por lo tanto resulta:
Veamos el caso práctico z = 2 + πi, ez sería:
Realmente, con un número imaginario puro estamos haciendo lo mismo. En el ejemplo del artículo anterior, la parte real es 0, y por lo tanto sería:
Como curiosidad, acabamos de trabajar con los números más importantes en matemáticas:
- El cero. Elemento neutro de la suma.
- El uno. Elemento neutro de la multiplicación.
- El número imaginario i.
- π (pi), la relación entre la longitud de una circunferencia y su diámetro.
- e, el límite de una sucesión:
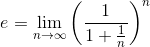
En el anterior artículo vimos la función exponencial en series de Taylor y al ser e = e1, podemos también definir e como el sumatorio de una serie:
E ora, ancora piu’ difficile! (Aunque no mucho más) ¿Cómo hacer el cálculo si la base es cualquier número real en vez de e? Eso lo veremos más adelante.
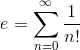
Pingback: Un número real elevado a un complejo | Víctor Iglesias
Como hallaría el módulo de e elevado a un número complejo?
Gracias por su trabajo …. Los numerous Complejos no son mis preferidos. pero toca aprender a manejarlos …. Me gustaria saber si me puede ayudar con una pregunta que nadie responde: Como se calculan los Ceros de la Hipotesis de Reimann? Que involugra precisamente los Numeros Complejos. ( le quedo debiendo las tildes)