El producto escalar es una operación entre dos vectores que retorna un escalar, es decir, un número real. Existen dos definiciones de esta operación que darán el mismo resultado, aunque inicialmente no sea muy intuitivo que así sea: la analítica y la geométrica. Veamos la primera de ellas:
Dados dos vectores del espacio vectorial ℝn, u = (u1, u2, …, un) y v = (v1, v2, …, vn), se define el producto escalar de ambos, u · v como:
u·v = u1 · v1 + u2 · v2 + … + un · vn
En todo espacio vectorial euclídeo, y por lo tanto normado, podemos usar también la definición geométrica, esta nos dice que el producto escalar de dos vectores es el producto del módulo (o norma) de cada uno de ellos por el coseno del ángulo que forman:
A continuación, veamos dos ejemplos sencillos en el plano cartesiano, ℝ2, para ver que ambas formas arrojan el mismo resultado. Ya nos advirtió Johan Cruyff: «Un palomo no hace verano», por lo que estos dos ejemplos no pretenden demostrar nada sino ejemplificar este concepto poco intuitivo. El primer ejemplo consistirá en los vectores u = (2, 2) y v = (2, -2):
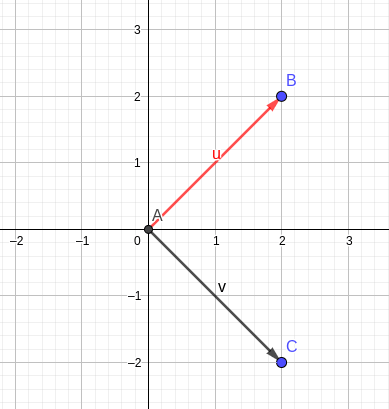 El ángulo entre ambos es, obviamente, 90º, pues cada uno hace un ángulo de 45º con el eje de las abscisas. Como cos(90º) = 0, según la segunda definición el producto escalar también es 0, pues cualquier número multiplicado por 0 es 0. El mismo resultado obtenemos con la forma analítica:
El ángulo entre ambos es, obviamente, 90º, pues cada uno hace un ángulo de 45º con el eje de las abscisas. Como cos(90º) = 0, según la segunda definición el producto escalar también es 0, pues cualquier número multiplicado por 0 es 0. El mismo resultado obtenemos con la forma analítica:
u·v =2·2 + 2·(-2) = 4 – 4 = 0
El segundo ejemplo estará constituido por los vectores u = (1, 1) y v = (2, 0):
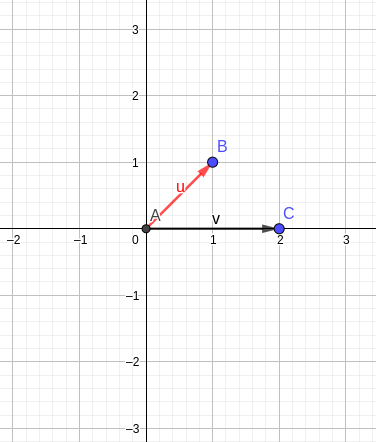 En este caso, el ángulo entre ambos es de 45º. El coseno de 45º es √2 / 2, no es tan redondo como el anterior, no obstante, ambas definiciones deben coincidir:
En este caso, el ángulo entre ambos es de 45º. El coseno de 45º es √2 / 2, no es tan redondo como el anterior, no obstante, ambas definiciones deben coincidir:
u·v = 1·2 + 1·0 = 2
Para poder calcular según la segunda definición necesitamos saber, en primer lugar, el módulo o norma de cada vector:
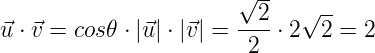 Finalmente, destacar dos aspectos de la definición geométrica. El primero de ellos es que nos permite obtener el ángulo que forman dos vectores pues, obviamente, al aislar el coseno en la ecuación (2) obtenemos:
Finalmente, destacar dos aspectos de la definición geométrica. El primero de ellos es que nos permite obtener el ángulo que forman dos vectores pues, obviamente, al aislar el coseno en la ecuación (2) obtenemos:
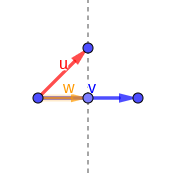
El segundo es que la interpretación geométrica del producto escalar de dos vectores es la proyección de uno sobre otro multiplicada por el módulo de este último. Con los vectores del último ejemplo, u = (1, 1) y v = (2, 0), la proyección de u sobre v sería:
w es un vector cuyo modulo es la distancia desde el origen hasta la proyección de u sobre v; la podemos calcular mediante trigonometría básica:
Atención: el módulo de w no es el producto escalar entre u y v. Para que lo sea, es necesario multiplicar por el módulo del segundo (v):
![]() Siendo esta exactamente la definición geométrica que vimos en la ecuación (2). En definitiva, podemos ver que:
Siendo esta exactamente la definición geométrica que vimos en la ecuación (2). En definitiva, podemos ver que:
Donde:
Esta fórmula no sale de la nada (aunque sí habrá salido en muchas chuletas), acabamos de ver que el vector w es la proyección del vector u sobre v, como sabemos que:
 Para aislar el módulo de w, olvidémonos del coseno y centrémonos en la segunda y tercera igualdad: multiplicando por el módulo de u en ambos lados de la ecuación nos resulta la fórmula de la proyección de u sobre v:
Para aislar el módulo de w, olvidémonos del coseno y centrémonos en la segunda y tercera igualdad: multiplicando por el módulo de u en ambos lados de la ecuación nos resulta la fórmula de la proyección de u sobre v:
 A modo de anécdota, para saber cuál es el vector w, debemos calcular el vector unitario de v, pues ambos van en la misma dirección, y multiplicarlo por |w|.
A modo de anécdota, para saber cuál es el vector w, debemos calcular el vector unitario de v, pues ambos van en la misma dirección, y multiplicarlo por |w|.
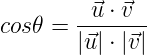
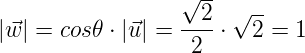
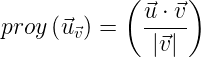
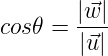
Una explicación que trata de llevar un concesto de análisis vectorial a sus bases cartesianas. Estas matemáticas son fundamentales por ejemplo en mi campo la Vectocardiografía. sin la cual no es posible entender un EKG
Buenas José,
Desconocía que también tuviera aplicaciones en cardiología. Desde hace unas semanas, tengo la intención de publicar otro artículo sobre el producto escalar, sólo falta encontrar un hueco para redactarlo. El mismo tratará sobre qué representa realmente el producto escalar, entender la noción «intuitiva» me parece fundamental para comprender las aplicaciones prácticas del mismo. En física, por ejemplo, es muy usado y a los alumnos se les enseña a aplicarlo sin pensar qué implica esta operación entre dos vectores, lo cual me parece lamentable pues precisamente se emplea en conceptos fundamentales de esta ciencia.
Un saludo y gracias por comentar.
El análisis vectorial es fundamental para comprender el EKG en Cardiologia
Pingback: Explicación intuitiva del producto escalar
Me parece que el concepto de proyección está expresado de manera errónea. La proyección de un vector en otro es un vector. Su modulo es la componente, el cual es una magnitud. Lo que se ha expresado en este artículo es la componente de un vector en otro, no su proyección. Debería revisarlo con detenimiento.
Buenas José Miguel,
En el artículo digo que la proyección de un vector sobre otro es también un vector, tanto por escrito como en la representación gráfica. En ningún momento se dice lo contrario.
Saludos.