En un artículo anterior acerca del producto escalar, se explicó detalladamente cómo se define matemáticamente esta operación. En la presente entrada se explicará qué representa realmente esta operación entre dos vectores, la noción «intuitiva» del mismo; algo imprescindible para entender qué estamos calculando realmente en otras ciencias (por ejemplo física) cuando es empleado.
Dados dos vectores, desde un punto de vista estrictamente matemático podríamos definir infinitas operaciones con ellos, por ejemplo el «producto payaso» de los vectores de n dimensiones u y v, se denota mediante u 🤡 v y se define así:
u 🤡 v = (u1·vn·|u|, u2·vn-1·|v|, u3·vn-2·|u|, …, un·v1·|v|)
Donde las coordenadas impares se multiplican por |u| y las pares por |v|.
Entonces, ¿por qué la operación conocida como producto escalar es importante? Un profesor de matemáticas podría responder a esta pregunta de sus alumnos afirmando que entenderán su importancia en la asignatura de física, donde es muy usado, pues tal vez en matemáticas no tenga un valor especial, pero esta respuesta es un tanto esquiva. La razón por la que es importante en física es precisamente por su interpretación geométrica (ergo matemática), pero esta sistemáticamente se omite, de manera que en física los alumnos deben resignarse a aplicarlo ciegamente.
La explicación a grosso modo no debería rehuirse pues no es ningún concepto especialmente complejo ni requiere de matemáticas «superiores»: el producto escalar de dos vectores, u·v, expresa «cuánto» de u «descansa» en la dirección de v, escalado al tamaño de v. (Esto ya se expresó sucintamente en el artículo anterior) Una vez expuesto esto, resulta mucho más intuitivo entender porqué en física se emplea para:
El trabajo
En la mítica representación del trabajo en Bachillerato:
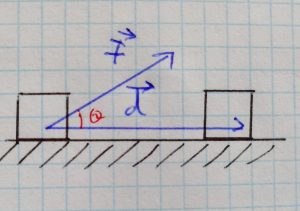
La fuerza aplicada no es paralela sino que forma un ángulo θ con el suelo, por lo que la única fuerza que realiza trabajo es la componente horizontal del vector fuerza, es decir:
Fx = cos θ · |F|
La caja se ha desplazado una distancia d y el trabajo realizado equivale a saber cuánto de F descansa en la dirección de d, escalado al tamaño de este último vector, si W designa el trabajo, sería:
El flujo de campo a través de una superficie
En física, un campo representa la distribución de una magnitud en cada uno de los puntos de una región del espacio. Los campos se pueden clasificar en varios tipos, entre ellos el escalar y el vectorial. El escalar asigna a cada punto del espacio una magnitud escalar, por ejemplo el mapa de presión atmosférica, donde cada isóbara une los puntos de igual presión atmosférica. El vectorial, que es el que aquí nos interesa, asigna a cada punto del espacio euclídeo una magnitud vectorial.
Dos campos vectoriales muy conocidos son el electrostático, formado por los vectores de la fuerza que recibiría una carga de prueba en cada punto del espacio afectado por la presencia de una o más cargas, y el campo de inducción magnética, cuyos vectores expresan en cada punto la fuerza debida a una corriente eléctrica que recibiría una carga en movimiento. En el primer caso, una o más cargas son las generadoras del campo, mientras que en el segundo es una corriente eléctrica quien lo genera.
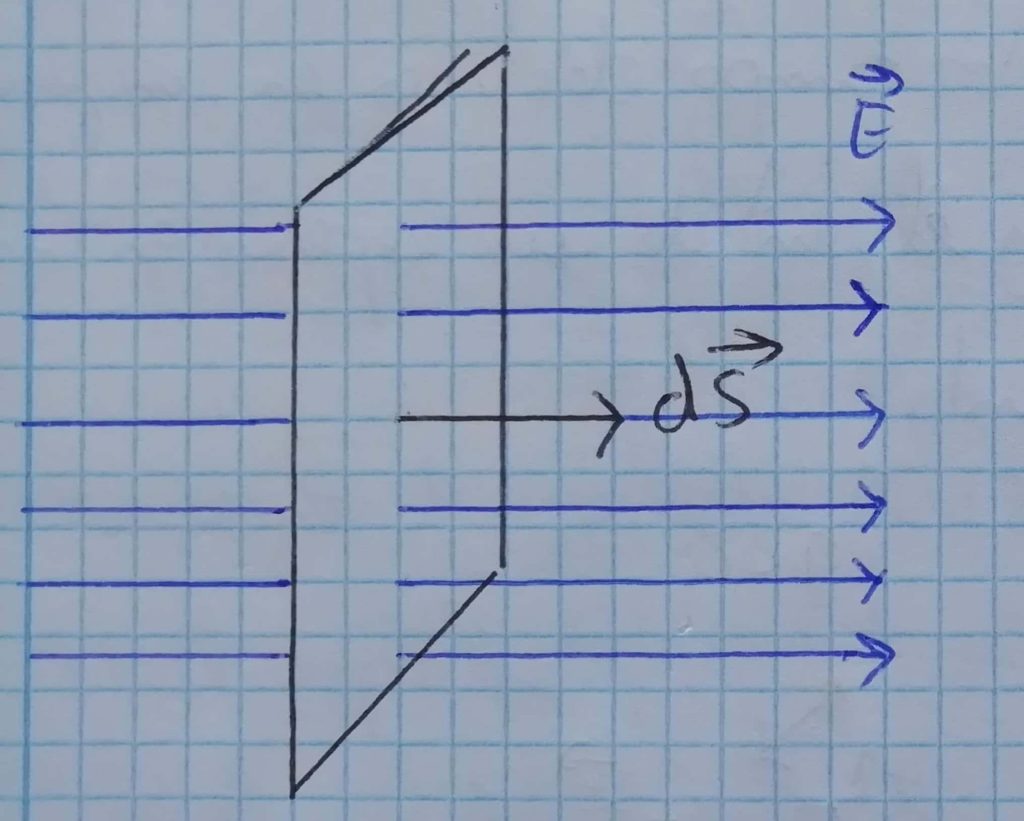
El concepto de flujo de campo es válido para todos los campos vectoriales, este expresa el campo que atraviesa una superficie mediante un escalar. En el caso del campo electrostático se calcula mediante:
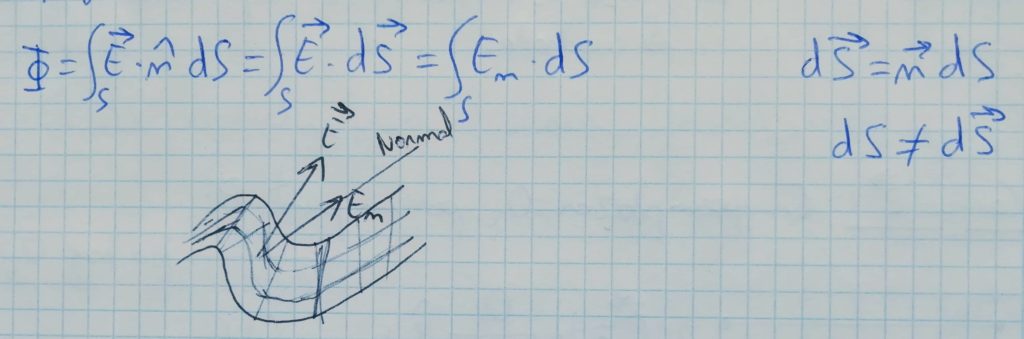 Donde n̂ es el vector normal en la superficie, se trata de un vector perpendicular a la superficie en cada punto y es unitario (tiene como módulo la unidad).
Donde n̂ es el vector normal en la superficie, se trata de un vector perpendicular a la superficie en cada punto y es unitario (tiene como módulo la unidad). ![]() es el vector del campo electrostático generado por la carga o cargas. La componente del campo que atraviesa la superficie es
es el vector del campo electrostático generado por la carga o cargas. La componente del campo que atraviesa la superficie es ![]()
![]() es el diferencial de superficie, «trozos» infinitamente pequeños de la misma. La integral representa la suma de todos los puntos de la superficie.
es el diferencial de superficie, «trozos» infinitamente pequeños de la misma. La integral representa la suma de todos los puntos de la superficie.
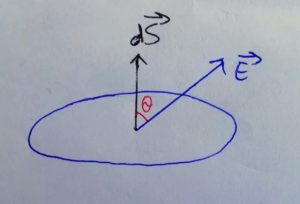
La superficie está representada por el vector d, su módulo es el área de la superficie, su dirección es perpendicular a la misma y su sentido hacia fuera.
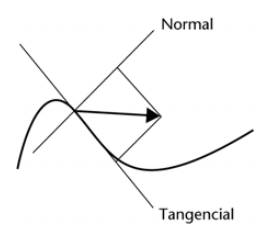
La razón por la que el campo que atraviesa una superficie se representa con un escalar es precisamente porque el flujo del campo electrostático sólo contempla la componente normal en la superficie, pues es la única que la atraviesa. Dada una curva o una superficie (curva o no), con un vector en un punto de la misma, este se puede descomponer como la suma de dos vectores:
- Uno tangente a la curva, llamado la componente tangencial del vector.
- Otro perpendicular a la curva, llamado la componente normal.
Esta descomposición es única.
A continuación, unos ejemplos en superficies simples:
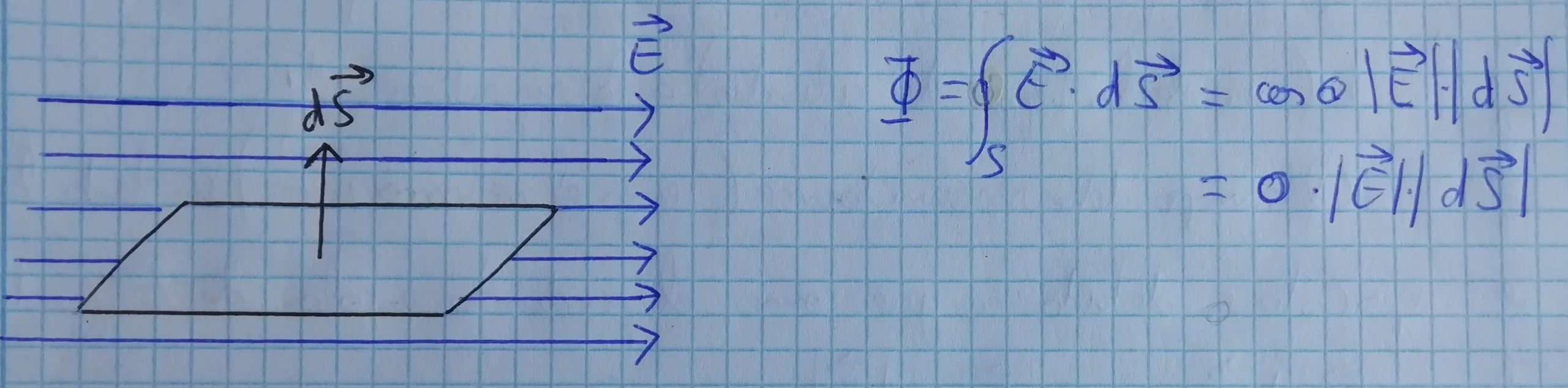
El ángulo que forman ambos vectores es de 90º, como su coseno es 0, el flujo a través de la superficie es 0 Nm²/C.
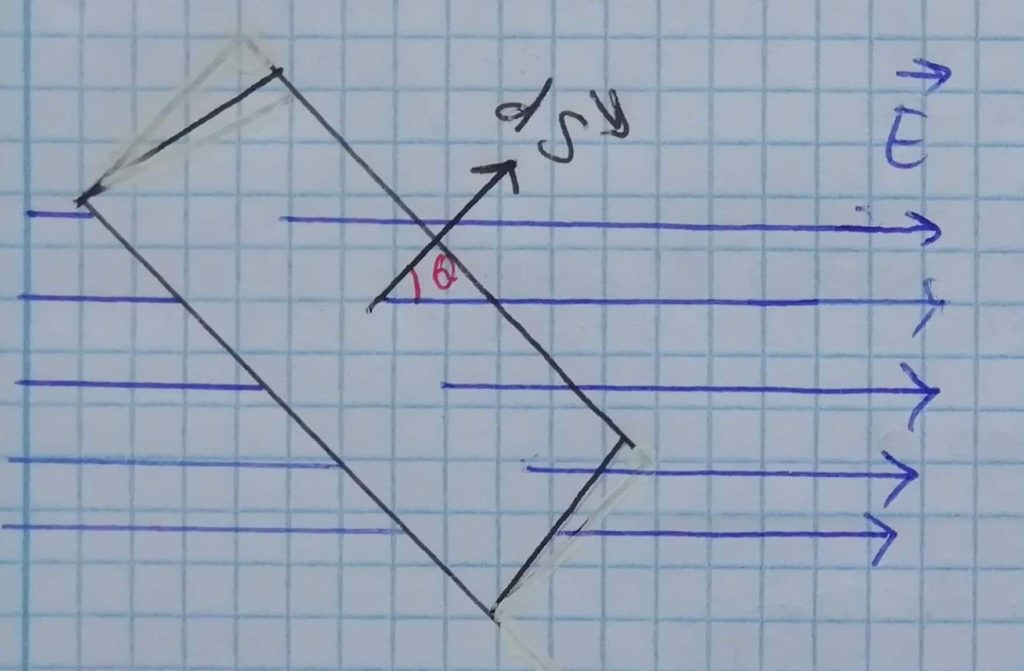
Si conocemos el ángulo θ podemos calcular el flujo de campo electrostático a través de la superficie.
Según nuestra explicación inicial a grosso modo, el flujo de campo eléctrico expresa «cuánto» del vector del campo electrostático «descansa» en la dirección de ![]() , escalado al tamaño de
, escalado al tamaño de ![]() , evaluado en toda la superficie.
, evaluado en toda la superficie.
Los mismos conceptos nos sirven para entender el flujo de inducción magnética, pues la ecuación es idéntica:
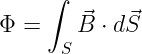 En general, toda la explicación de flujo de campo electrostático y su producto escalar, tal y como se ha dicho anteriormente, se puede aplicar a todos los flujos de campos vectoriales a través de una superficie.
En general, toda la explicación de flujo de campo electrostático y su producto escalar, tal y como se ha dicho anteriormente, se puede aplicar a todos los flujos de campos vectoriales a través de una superficie.
Ambas fórmulas pueden aceptarse ciegamente como la forma de calcular el flujo, o bien entender mejor cómo y qué se está calculando si profundizamos en el uso que hacen del producto escalar.
En definitiva, el producto escalar aparece en diversas ocasiones durante el transcurso del Bachillerato, en la asignatura de física y en la de matemáticas, pero en ninguna acostumbra a haber tiempo para explicar su interpretación geométrica, esperando el profesor de una asignatura que lo explique el de la otra. Como se ha visto, su significado no es complejo y entenderlo sirve para no aplicar las fórmulas mediante un «acto de fe», sino entendiendo un poco mejor el porqué de las mismas.

Muy interesante. Es evidente que explicar el significado de la cosas ayuda a asimilarlas. En matemáticas el producto escalar permite definir una distancia y, por tanto, una métrica en cualquier espacio vectorial. En particular, toda métrica lleva asociada una matriz simétrica y definida positiva. Recíprocamente, toda matriz simétrica y definida positiva da lugar a una métrica y a un producto escalar. Tiene especial interés la métrica de Minkowski con matriz
-1
0 1
0 0 1
0 0 0 1
que se utiliza en la relatividad especial.