En la anterior entrada estimé el crecimiento de casos en España a partir de un titular de un diario, en el presente se pretende hacer una estimación mejor fundamentada. En todo caso, ni en el anterior ni en el presente artículo estoy haciendo nada más que un pasatiempo, sin mayores pretensiones. Una vez aclarado que para cualquier estudio serio del tema deben consultarse fuentes oficiales, podemos empezar. En primer lugar, vamos a trabajar con los datos que proporciona el Ministerio de Sanidad del Gobierno de España:
| Fecha | Día | Casos | Ln(Casos) |
| 24/02/20 | 1 | 4 | 1,3862943611 |
| 25/02/20 | 2 | 8 | 2,0794415417 |
| 26/02/20 | 3 | 14 | 2,6390573296 |
| 27/02/20 | 4 | 26 | 3,258096538 |
| 28/02/20 | 5 | 45 | 3,8066624898 |
| 29/02/20 | 6 | 59 | 4,0775374439 |
| 01/03/20 | 7 | 84 | 4,4308167988 |
| 02/03/20 | 8 | 125 | 4,8283137373 |
| 03/03/20 | 9 | 169 | 5,1298987149 |
| 04/03/20 | 10 | 228 | 5,429345629 |
| 05/03/20 | 11 | 282 | 5,6419070709 |
| 06/03/20 | 12 | 365 | 5,8998973536 |
| 07/03/20 | 13 | 430 | 6,0637852087 |
| 08/03/20 | 14 | 674 | 6,5132301109 |
| 09/03/20 | 15 | 1231 | 7,1155821262 |
| 10/03/20 | 16 | 1695 | 7,4354380198 |
| 11/03/20 | 17 | 2277 | 7,7306140661 |
| 12/03/20 | 18 | 3146 | 8,0538870836 |
| 13/03/20 | 19 | 5232 | 8,5625488931 |
| 14/03/20 | 20 | 6332 | 8,753371421 |
| 15/03/20 | 21 | 7844 | 8,9675041873 |
| 16/03/20 | 22 | 9942 | 9,2045234867 |
| 17/03/20 | 23 | 11178 | 9,3217028398 |
| 18/03/20 | 24 | 14769 | 9,6002856684 |
| 19/03/20 | 25 | 18077 | 9,802395691 |
| 20/03/20 | 26 | 20410 | 9,9237802558 |
| 21/03/20 | 27 | 25374 | 10,1414803067 |
| 22/03/20 | 28 | 28768 | 10,2670189373 |
| 23/03/20 | 29 | 33089 | 10,4069561798 |
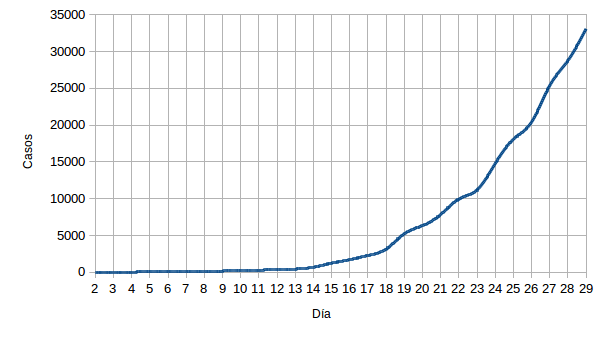
Las columnas «Fecha» y «Casos» son los datos oficiales, mientras que las columnas «Día» y «Ln(Casos)» se han añadido para realizar las estimaciones. Desde los medios de comunicación se repite que el crecimiento es exponencial, algo que podemos comprobar que es cierto si hacemos una representación gráfica a partir de los datos de la tabla:
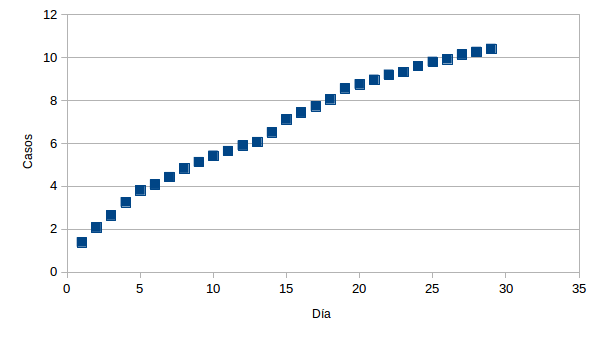
Por lo tanto, al tratarse de una función exponencial, al aplicar el logaritmo sobre cada número de casos deberíamos obtener una nube de puntos que se aproxima muy bien por una línea recta. En estos casos suele usarse el logaritmo natural, es decir, en base e, aunque el objetivo se consigue independientemente de la base empleada; la única diferencia sería la escala: a mayor base menor sería la escala. Desconozco porqué se emplea el logaritmo natural, puede que esté relacionado con el hecho de que la función inversa de f(x) = ln(x), la exponencial f(x) = ex, tenga la peculiaridad de que la función que da el área de la función en un punto x venga dada también por f(x) = ex y eso pueda simplificar ciertos cálculos. En todo caso, este es el resultado:
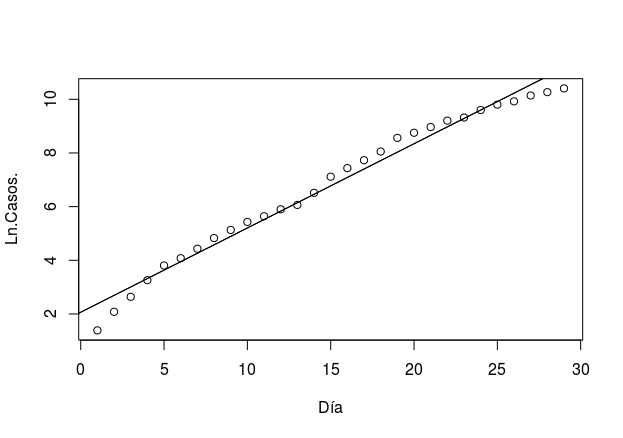
A partir de las columnas «Casos» y «Ln(Casos)» podemos obtener la recta de regresión lineal. Para ello existen diferentes programas, como por ejemplo Excel, pero en este caso emplearemos el software estadístico R y obtenemos el siguiente gráfico:
También obtenemos algo aún más importante: los parámetros de la recta β0 y β1, es decir, la pendiente y la ordenada en el origen o término independiente. (*)
lm(formula = casosln$Ln.Casos ~ casosln$Día)
Coefficients:
(Intercept) casosln$Día
2.0639 0.3141
Es decir, la función es f(x) = 0,3141x + 2,0639
Para obtener la función que aproxima la exponencial (1) y que nos permitirá conocer la evolución futura del número de casos debemos recordar que esta recta de regresión en realidad representa esto: Ln(Casos) = 0,3141d + 2,0639, donde d es el número de día. Si hacemos la función inversa:
Ya tenemos la función que nos permite aproximar la evolución futura del número de infectados. Eso sí, de forma muy aproximada, pues parece ser que la fluctuación de la cantidad de unidades de test disponibles (siempre escasa) hace que los datos deban ser cogidos con pinzas. Veamos qué tal se comporta nuestra aproximación contra los datos reales y vamos a estirarla un poco para intentar predecir el futuro:
| Fecha | Día | Casos | Aproximación |
| 24/02/20 | 1 | 4 | 10,7832751725 |
| 25/02/20 | 2 | 8 | 14,7625908953 |
| 26/02/20 | 3 | 14 | 20,2103800983 |
| 27/02/20 | 4 | 26 | 27,6685486049 |
| 28/02/20 | 5 | 45 | 37,878979919 |
| 29/02/20 | 6 | 59 | 51,8573323159 |
| 01/03/20 | 7 | 84 | 70,9940690239 |
| 02/03/20 | 8 | 125 | 97,1927712338 |
| 03/03/20 | 9 | 169 | 133,0594922924 |
| 04/03/20 | 10 | 228 | 182,1619886374 |
| 05/03/20 | 11 | 282 | 249,3846138493 |
| 06/03/20 | 12 | 365 | 341,4141780619 |
| 07/03/20 | 13 | 430 | 467,405102434 |
| 08/03/20 | 14 | 674 | 639,8900333358 |
| 09/03/20 | 15 | 1231 | 876,0264974221 |
| 10/03/20 | 16 | 1695 | 1199,303605629 |
| 11/03/20 | 17 | 2277 | 1641,8785763983 |
| 12/03/20 | 18 | 3146 | 2247,7754981999 |
| 13/03/20 | 19 | 5232 | 3077,2645206148 |
| 14/03/20 | 20 | 6332 | 4212,8570835557 |
| 15/03/20 | 21 | 7844 | 5767,5135457383 |
| 16/03/20 | 22 | 9942 | 7895,8796466457 |
| 17/03/20 | 23 | 11178 | 10809,6695222122 |
| 18/03/20 | 24 | 14769 | 14798,7254629804 |
| 19/03/20 | 25 | 18077 | 20259,8492838888 |
| 20/03/20 | 26 | 20410 | 27736,273237359 |
| 21/03/20 | 27 | 25374 | 37971,6967445167 |
| 22/03/20 | 28 | 28768 | 51984,2641193576 |
| 23/03/20 | 29 | 33089 | 71167,8420433336 |
| 24/03/20 | 30 | 97430,6711253196 | |
| 25/03/20 | 31 | 133385,183579827 | |
| 26/03/20 | 32 | 182607,868683772 |
Vemos que nuestra función aproxima bastante bien hasta el 19 de marzo y que a partir de aquí se empieza a alejar bastante de la realidad. Teniendo en cuenta que la cuarentena empezó el 14 de marzo con el decreto de alarma nacional, esta desconexión con la realidad puede deberse a que la cuarentena esté surgiendo efecto, o bien a una escasez de test realizados. Esperemos que sea debido a lo primero.
Para calcular el factor de aumento diario procedemos así:
e0,3141 = 1 + r → r = e0,3141 – 1 ≈ 0,369027
En consecuencia, la siguiente función es equivalente a la anterior:
Casos = 7,8766·(1 + 0,369027)d = 7,8766·1,369027d
En conclusión, el crecimiento de estos pasados días ha sido del 36,9% diario, y podemos afirmar que la evolución está siendo bastante peor que ese 20% que aparecía en el titular de La Vanguardia el 8 de marzo.
Asimismo, proporciona el coeficiente de determinación, R2, que en este caso es de 0,9803; un valor elevado que nos indica que el ajuste es bastante bueno, como cabía esperar después de la aplicación del logaritmo.
Muy bueno. De lo mejor que he leído sobre la evolución del coronavirus
Molt bo ! Hi ha qui s’ho pren en serio !
Muchas gracias. Me alegra que el artículo sea de vuestro interés.
He recibido este mensaje de una lectora a través del formulario de contacto. Lo dejo aquí en forma de comentario pues me parece de interés general, así se lo he comunicado a María y no ha mostrado ningún inconveniente.
Hola –
Te escribo porque siento que esta información te puede importar a ti y a tus lectores.
Mi nombre es Maria, y primero que todo, quiero agradecerte por la información que compartiste sobre el Coronavirus (COVID-19) acá: victoriglesias.net/
No encontré ningún tipo de datos/cifras sobre el Coronavirus en tu país (y el resto del mundo), y decidí buscar en Google información en donde se muestran datos reales (¡Y me pareció muy confuso!).
Lo que es más importante es basar la información en números verificados de la Organización Mundial de la Salud que proporcionó los datos a esta herramienta:
https://es.safetydetectives.com/novel-coronavirus-ncov-real-time-report/
Quiero recomendarte que lo agregues como recurso para tu página, para así ayudar a otros (como a mi) a obtener números reales sobre tu país y el resto del mundo.
Sigan haciendo tan buen trabajo,