Archivo de la categoría: PHP

Entradas del blog acerca del lenguaje de programación PHP, uno de los mejores para el desarrollo web.

Debug en la barra de Symfony desde Twig

Posted on por
Responder

Este es un pequeño truco para que el volcado mediante dump() de una variable en Twig no aparezca en medio del HTML sino que lo haga en la barra de Symfony, tal y como sucede cuando el volcado se hace desde el código PHP (por ejemplo en un controlador, entidad, etc.) Curiosamente, esto no aparece en la documentación de Twig, de ahí el nombre de «truco».

Los ejemplos de uso que aparecen:

{{ dump(app.request.locale) }}

Pueden llegar a provocar un molesto resultado:

dump en el html

En cambio, si lo tratamos como una instrucción más mediante {% en vez de {{, el resultado se mostrará en el profiler de Symfony:

{% dump(app.request.locale) %}


Lo cual nos facilitará la vida en algunas circunstancias.

Optimizaciones inútiles del código en PHP

Posted on por
Responder

En las aplicaciones donde la velocidad no es determinante – categoría a la que pertenecen muchas aplicaciones web – el código, antes que optimizado, debe estar estructurado. Como los requerimientos están cambiando frecuentemente, el tiempo del programador es mucho más importante (y costoso) que el tiempo de CPU. Además, lo que puede parecernos una optimización, a veces no lo es. Veamos un ejemplo con los desplazadores de bits.

La teoría nos dice que tanto la operación de multiplicación como la de división requieren cierto tiempo de computación, especialmente esta última. Ahora bien, si esta operación se hace con una potencia de 2, se convierte en algo trivial para la CPU gracias a los desplazadores, unos sencillos bloques combinacionales formados por unas pocas puertas lógicas.

Los desplazadores tienen una señal de entrada y una de salida de n bits ambas. La señas de salida se obtiene desplazando los bits de entrada m veces hacia la derecha o hacia la izquierda El desplazamiento a la izquierda equivale a multiplicar por 2m mientras que a la derecha realiza la división entera por 2m. En el caso del desplazamiento a la derecha o división, en función del valor que se asigne a los «nuevos» bits, existen dos tipos de desplazadores:

  • Lógicos: Se ponen a 0.
  • Aritméticos: Se ponen al mismo valor que el bit de más peso de la entrada. Sirven para que los números codificados en complemento a dos conserven el signo.
Desplazador aritmético y lógico de 4 bits

Dos desplazadores de 4 bits: El de arriba lógico y el de abajo aritmético. Ambos desplazan 01 (2(10) bits a la derecha, i.e., dividen por 2.

Sigue leyendo →

Cómo simplificar una relación Many-To-Many consigo misma

Posted on por
1

En esta breve entrada expongo cómo el programador puede facilitarse un poco su actividad cuando en Doctrine establezca una relación de una entidad consigo misma. El código que se expone es de una entidad del framework Symfony, pero fácilmente se puede adaptar a cualquier entorno PHP donde, eso sí, se esté empleando este conocido ORM.

Según la documentación de Doctrine, el código para la relación Many-To-Many (de muchos a muchos) de una entidad que se referencia a si misma, por ejemplo un producto que puede tener otros productos relacionados, sería:

class Product
{
    /**
     * @ORM\Id()
     * @ORM\GeneratedValue()
     * @ORM\Column(type="integer")
     */
    private $id;

    /**
     * @ManyToMany(targetEntity="Product", mappedBy="myProducts")
     */
    private $relatedWithMe;

    /**
     * @ManyToMany(targetEntity="Product", inversedBy="relatedWithMe", fetch="EAGER")
     * @JoinTable(name="related_products",
     *      joinColumns={@JoinColumn(name="product_id", referencedColumnName="id")},
     *      inverseJoinColumns={@JoinColumn(name="related_product_id", referencedColumnName="id")}
     *      )
     */
    private $myProducts;

    public function __construct()
    {
        $this->relatedWithMe = new ArrayCollection();
        $this->myProducts = new ArrayCollection();
    }

    public function addRelatedWithMe(Product $relatedWithMe): self
    {
        if (!$this->relatedWithMe->contains($relatedWithMe)) {
            $this->relatedWithMe[] = $relatedWithMe;
            $relatedWithMe->addMyProduct($this);
        }

        return $this;
    }

    public function removeRelatedWithMe(Product $relatedWithMe): self
    {
        if ($this->relatedWithMe->contains($relatedWithMe)) {
            $this->relatedWithMe->removeElement($relatedWithMe);
            $relatedWithMe->removeMyProduct($this);
        }

        return $this;
    }

    /**
     * @return Collection|Product[]
     */
    public function getMyProducts(): ?Collection
    {
        return $this->myProducts;
    }

    public function addMyProduct(Product $myProduct): self
    {
        if (!$this->myProducts->contains($myProduct)) {
            $this->myProducts[] = $myProduct;
        }

        return $this;
    }

    public function removeMyProduct(Product $myProduct): self
    {
        if ($this->myProducts->contains($myProduct)) {
            $this->myProducts->removeElement($myProduct);
        }

        return $this;
    }

Sigue leyendo →

Redimensión de imágenes proporcionalmente en PHP

Posted on por
5

Una necesidad que surge en todas las webs cuyos contenidos son introducidos por un usuario (o varios) a través de un gestor de contenidos, es adaptar las imágenes que estos suben al diseño de la misma para que no se deforme. Además, las proporciones de una imagen en una sección pueden ser diferentes a cómo se muestra en otra; un caso típico es usar una proporción para un listado y otra para la ficha de cada elemento, por ejemplo las noticias, los productos, etc.

Para resolver este problema sirve el conjunto de clases PHP que presentó en este artículo. Este software, a partir de una imagen original, creará una copia por cada tamaño que necesitemos. El proyecto completo puede verse en Github y el objetivo del presente artículo es explicar cómo funciona. En primer lugar, instanciamos la clase:

$objResize = Signia_ImageResize_Factory::getInstanceOf($srcFile, $destFile, $newSize);

Donde:

  • $srcFile es el path hacia la imagen que ha subido el usuario.
  • $desFile es el path de la imagen de destino.
  • $newSize es el tamaño deseado.

A partir de un array con los tamaños deseados podemos crear un bucle por cada uno de ellos ($newSize). Los índices widthMax y heigthMax hacen referencia al tamaño máximo permitido, mientras que width y height pueden entenderse como widthMin y heightMin. Veamos un ejemplo:

$imageType = [
  'slide' => ['width' => 1000, 'widthMax' => 1000, 'height' => 400, 'heightMax' => 400, 'background' => '000000'],
  'r2_34' => ['width' => 468, 'widthMax' => 2340, 'height' => 200, 'heightMax' => 1000],
  'r2_7'  => ['width' => 1080, 'widthMax' => 2700, 'height' => 400, 'heightMax' => 1000],
  'r1_6'  => ['width' => 459, 'widthMax' => 1000, 'height' => 287, 'heightMax' => 625],
  'r1'    => ['width' => 266, 'widthMax' => 266, 'height' => 177, 'heightMax' => 177]
];

En Factory.php podemos ver la clase Signia_ImageResize_Factory:

class Signia_ImageResize_Factory
{
	static public function getInstanceOf($srcImageName, $destImageName, $newSize)
	{
		$aux       = explode(".", $destImageName);
		$extension = end($aux);
		if (preg_match("/jpg|JPG|jpeg|JPEG/", $extension)) {
			$extension = "jpeg";
		}
		$imageResizer = "Signia_ImageResize_" . ucfirst($extension);

		return new $imageResizer($srcImageName, $destImageName, $newSize);
	}
}

Sigue leyendo →

Funciones de orden superior

Posted on por
4

Tanto en matemáticas como en informática, las funciones de orden superior son aquellas que cumplen, al menos, una de estas condiciones:

  1. Esperan como argumento/s una o más funciones.
  2. Devuelven una función como resultado.

Ejemplos en matemáticas son la derivada y la antiderivada o función primitiva.

operador diferencial

El operador diferencial es una función de orden superior

Antiderivada

La antiderivada de una función f es una función F tal que F’ = f

En informática son la esencia de los lenguajes funcionales, pero también aparecen en lenguajes de otros paradigmas. Este es un ejemplo en el lenguaje Scheme en el que la función (f x) recibe un argumento y devuelve una función:

(define (f x)
  (lambda (y) (+ x y)))
(display ((f 3) 7))

Puede ejecutarse aquí para ver el resultado.

Cuando nació Javascript, a algunos programadores les pareció un lenguaje orientado a objetos fallido1, sobretodo porque, por razones comerciales, se le puso un nombre que lo asocia con Java. Desconozco si su creador estuvo muy de acuerdo con ese nombre pues, tal y como se diseño este lenguaje, da bastante juego a la programación funcional. En el siguiente ejemplo, el método filter() es una función de orden superior, pues espera recibir una función como parámetro:

function isPrime(x){
  if (x === 2) {
     return true;
  }
  let test = x%2 !== 0;
  let i = 3;
  stop = Math.floor(Math.sqrt(x)); // Raíz entera de x
  while (test && i <= stop) {
	  test = x%i !== 0;
	  i = i + 2;
  }
  return test;
}

const numbers = [47, 139, 137, 213, 2, 3, 45, 1515];
const primeNumbers = numbers.filter(isPrime);
console.log(primeNumbers);

Lo que este programa hace es filtrar la formación de números naturales «numbers«, dejando sólo los que sean primos en «primeNumbers«. Cada elemento de «numbers» será evaluado por la función «isPrime» mediante la criba de Eratóstenes. El lector puede ejecutarlo accediendo a la consola del navegador pulsando F12 y modificar el valor de «numbers» con los números (o el número) que quiera saber si son primos o no.

Este tipo de funciones están en prácticamente todos los lenguajes modernos, incluso en los que no se tuvo en cuenta el paradigma funcional en el momento de su creación. Es el caso de PHP, donde podemos encontrar una gran cantidad de funciones que esperan otra función, como es el caso de, por ejemplo, preg_replace_callback()2:

$capitalice = function($coincidencia) {
    return strtoupper($coincidencia[1]);
};

echo preg_replace_callback('~-([a-z])~', $capitalice, 'hola-mundo');

Además de usar las implementadas en funciones y métodos propios del lenguaje, también podemos crear las nuestras, de forma parecida a un lenguaje completamente funcional. En Javascript, la Wikipedia nos ofrece el siguiente ejemplo:

const twice = (f, v) => f(f(v));
const add3 = v => v + 3;

console.log(twice(add3, 7));

Lo mismo es posible en PHP:

$twice = function($f, $v) {
    return $f($f($v));
};

$f = function($v) {
    return $v + 3;
};

echo($twice($f, 7));

La programación funcional pretende tratar la programación como la evaluación de funciones matemáticas, paradigma muy diferente a la programación imperativa, basada en estados y en instrucciones que lo cambian. Tal vez las características funcionales que tienen algunos lenguajes puedan ayudarnos a introducirnos en un paradigma, el funcional, que nos exige una forma muy distinta de enfocar los problemas.

 

1 Todavía hoy en día, y a pesar de los cambios que ha sufrido en los últimos ECMA, sigue despertando las críticas de los programadores que, debido a su nombre, esperan que se comporte como un lenguaje completamente orientado a objetos, como Java, y se dan de bruces contra la realidad.

2 El parámetro que recibe la función contenida en $capitalize son las coincidencias que encuentre la expresión regular.

Decimales del número e por Taylor

Posted on por
2

Tanto Jhon von Neumann como Steve Wozniack hicieron el ejercicio de encontrar miles de decimales del número e, en el ENIAC (uno de los primeros ordenadores de propósito general) y en un Apple II, respectivamente. Si personas de tan elevado tamaño intelectual consideraron oportuno hacerlo, ¿quién soy yo para contrariarlos? Así que, salvando las distancias, me he decidido a hacerlo.

El método empleado han sido las series de Taylor. Para el mismo, se requiere calcular el factorial, la siguiente función recursiva lo calcula para el número recibido como parámetro:

function factorial(a) {
  if (a === 0) {
      return 1;
  }else{
      return a * factorial(a - 1);
  }
}

El siguiente código Javascript calcula, a partir del polinomio de Taylor1 de grado 20 en torno al punto a=0, es decir, e1, unos cuantos decimales:

function factorial(a) {
  if (a === 0) {
      return 1;
  }else{
      return a * factorial(a - 1);
  }
}

var e = 1;

for (i = 1; i <= 19; i++) {
   e = e + 1/factorial(i);
}
console.log(e);

El lector puede copiar el código y ejecutarlo en el mismo navegador con el que está leyendo este artículo, presionando F12 y accediendo a la consola:

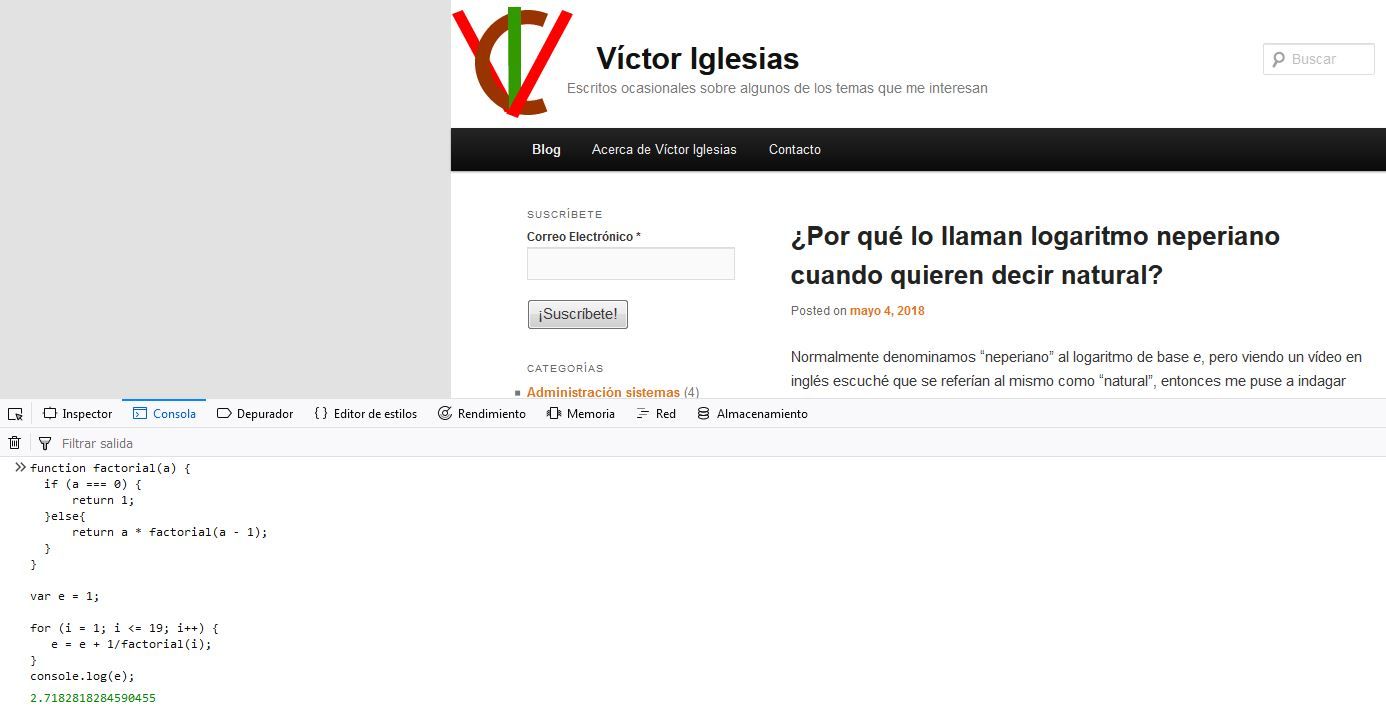
Decimales de e en Javascript por Taylor

Decimales de e en Javascript por Taylor. Ejecutado en Firefox.

Por culpa del uso de la coma flotante que hace Javascript (ya incluido en el microprocesador), no podemos sacar más decimales, pues el resultado será redondeado al que vemos en la imagen. Para salvar este inconveniente, en PHP existe la librería BC Math, que nos permite trabajar con números de – casi – cualquier tamaño y precisión. Para que después digan que es un lenguaje de juguete… Éste es el código:

<?php

function factorial($a) {
  if ($a === 0) {
      return 1;
  }else{
      return bcmul($a, factorial($a - 1), 3000);
  }
}

$e = '2';

for ($i = 2; $i <= 1000; $i++) {
   $e = bcadd($e, bcdiv('1', factorial($i), 3000), 3000);
}
echo ($e);

Con el que se obtienen 2572 dígitos correctos:

2.71828182845904523536028747135266249775724709369995957496696762772407663035354759457138217852516642742746639193200305992181741359662904357290033429526059563073813232862794349076323382988075319525101901157383418793070215408914993488416750924476146066808226480016847741185374234544243710753907774499206955170276183860626133138458300075204493382656029760673711320070932870912744374704723069697720931014169283681902551510865746377211125238978442505695369677078544996996794686445490598793163688923009879312773617821542499922957635148220826989519366803318252886939849646510582093923982948879332036250944311730123819706841614039701983767932068328237646480429531180232878250981945581530175671736133206981125099618188159304169035159888851934580727386673858942287922849989208680582574927961048419844436346324496848756023362482704197862320900216099023530436994184914631409343173814364054625315209618369088870701676839642437814059271456354906130310720851038375051011574770417189861068739696552126715468895703503540212340784981933432106817012100562788023519303322474501585390473041995777709350366041699732972508868769664035557071622684471625607988265178713419512466520103059212366771943252786753985589448969709640975459185695638023637016211204774272283648961342251644507818244235294863637214174023889344124796357437026375529444833799801612549227850925778256209262264832627793338656648162772516401910590049164499828931505660472580277863186415519565324425869829469593080191529872117255634754639644791014590409058629849679128740687050489585867174798546677575732056812884592054133405392200011378630094556068816674001698420558040336379537645203040243225661352783695117788386387443966253224985065499588623428189970773327617178392803494650143455889707194258639877275471096295374152111513683506275260232648472870392076431005958411661205452970302364725492966693811513732275364509888903136020572481765851180630364428123149655070475102544650117272115551948668508003685322818315219600373562527944951582841882947876108526398139559900673764829224437528718462457803619298197139914756448826260390338144182326251509748279877799643730899703888677822713836057729788241256119071766394650706330452795466185509666618566470971134447401607046262156807174818778443714369882185596709591025968620023537185887485696522000503117343920732113908032936344797273559552773490717837934216370120500545132638354400018632399149070547977805669785335804896690629511943247309958765523681285904138324116072260299833053537087613893963917795745401613722361878936526053815584158718692553860616477983402543512843961294603529133259

Aquí está el link que ejecuta este código:

https://www.victoriglesias.net/e.php

Al seguir el link, el lector con interés en el tema descubrirá que proporciona más decimales, pero, como dije, sólo los primeros 2572 son correctos. Supongamos que sabemos que e está por debajo de 3, pero no podemos concretar más, el error, por el residuo del teorema de Taylor, sería 3/(i + 1)!, es decir:

+-0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000744805637342692...

Por cierto, no por acotar mejor e, por ejemplo 2’8, dejaríamos de obtener menos posiciones a 0 hasta obtener los primeros decimales del error. 2’8/(i + 1)! es:

+-0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000695151928186513...

Por lo tanto, aunque acotemos con más precisión e, la fórmula del residuo nos sigue asegurando que hemos calculado correctamente la misma cantidad de decimales.

Si parecen insuficientes y se desea mayor precisión, bastará con incrementar el tope de la variable i del bucle a más de 1000. Eso sí, si nos tomamos este cálculo en serio, sería aconsejable optimizar previamente la función recursiva.

En definitiva, aunque me quedé muy lejos del récord mundial ;-), fue entretenido hacerlo y espero que al lector le parezca interesante también o, por lo menos, curioso.

1 Se llama serie de Maclaurin el caso concreto de Taylor a=0