En las aplicaciones donde la velocidad no es determinante – categoría a la que pertenecen muchas aplicaciones web – el código, antes que optimizado, debe estar estructurado. Como los requerimientos están cambiando frecuentemente, el tiempo del programador es mucho más importante (y costoso) que el tiempo de CPU. Además, lo que puede parecernos una optimización, a veces no lo es. Veamos un ejemplo con los desplazadores de bits.
La teoría nos dice que tanto la operación de multiplicación como la de división requieren cierto tiempo de computación, especialmente esta última. Ahora bien, si esta operación se hace con una potencia de 2, se convierte en algo trivial para la CPU gracias a los desplazadores, unos sencillos bloques combinacionales formados por unas pocas puertas lógicas.
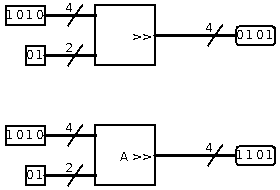
Los desplazadores tienen una señal de entrada y una de salida de n bits ambas. La señas de salida se obtiene desplazando los bits de entrada m veces hacia la derecha o hacia la izquierda El desplazamiento a la izquierda equivale a multiplicar por 2m mientras que a la derecha realiza la división entera por 2m. En el caso del desplazamiento a la derecha o división, en función del valor que se asigne a los «nuevos» bits, existen dos tipos de desplazadores:
- Lógicos: Se ponen a 0.
- Aritméticos: Se ponen al mismo valor que el bit de más peso de la entrada. Sirven para que los números codificados en complemento a dos conserven el signo.
Dos desplazadores de 4 bits: El de arriba lógico y el de abajo aritmético. Ambos desplazan 01 (2(10) bits a la derecha, i.e., dividen por 2.
