Programador Python en San Valentín
Programador Python en San Valentín
Imagen
Responder
Archivo de la categoría: Programación
Cómo el compilador JIT de Java mejora la velocidad de ejecución
Históricamente, los lenguajes siempre se habían dividido entre interpretados y compilados, en lo que se refiere a su ejecución. A día de hoy, con los compiladores JIT se crea una nueva categoría: los lenguajes que son una combinación de ambos. Los compiladores JIT son omnipresentes, por ejemplo los navegadores modernos disponen de uno para el lenguaje Javascript. También las máquinas virtuales de Java han evolucionado para incluir esta técnica, y es el caso concreto en el que se va a profundizar en este artículo.
Las implementaciones modernas de Java emplean un proceso de compilación dividido en dos pasos en el cual se produce una compilación en tiempo de ejecución, es decir, las máquinas virtuales de Java actuales disponen de un compilador JIT, just-in-time por sus siglas en inglés. En primer lugar, el compilador de Java compila en bytecode el código fuente, este bytecode es independiente de la plataforma de hardware donde se ejecuta. La máquina virtual de Java (JVM) es la encargada de ejecutar (interpretar mediante un intérprete) este bytecode. La máquina virtual sí es dependiente de la plataforma: Cada plataforma requiere de su propia máquina virtual para poder ejecutar el bytecode.
El compilador JIT de la máquina virtual es el encargado de detectar partes de este bytecode que se están ejecutando con mucha frecuencia y compilarlas al código máquina de la CPU de la plataforma para aumentar la velocidad de ejecución. El componente del compilador JIT encargado de detectar estos «puntos calientes» («hotspots» o «hot code» en inglés) del código es el profiler. Además, lo realiza en tiempo de ejecución, es decir, a medida que el programa se está ejecutando, detecta cuáles nuevas partes del código se han calentado y cuáles se han enfriado. De esta manera se supera la principal ineficiencia de los intérpretes: cuando código que se está ejecutando de forma reiterada (por ejemplo debido a un bucle while / for) debe ser interpretado una y otra vez. Además, esta característica es realmente potente, pues consigue que determinados tipos de programas se ejecuten más rápido que su equivalente en un lenguaje compilado orientado a objetos.
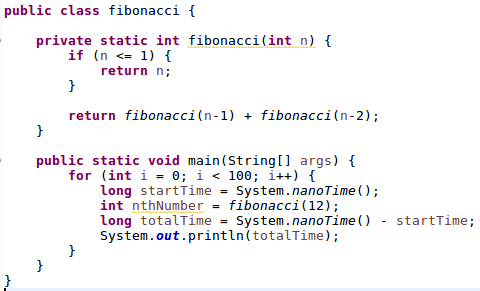
Para ver un caso concreto de cómo se optimiza en tiempo de ejecución un programa realizado en Java, pongamos a trabajar al ordenador: calculará 100 veces el número situado en la duodécima posición de la serie de Fibonacci, una forma como otra cualquiera de poner a calcular un ordenador. Este número es el 144, pero lo que realmente nos interesa es el tiempo transcurrido en cada una de las 100 ejecuciones.
Aritmética modular para entender el complemento a 2
Los ordenadores codifican internamente los números en binario. Los enteros pueden representarse mediante dos sistemas de representación: el complemento a 2 (Ca2 para abreviar) y el de signo y magnitud. Para los humanos es más amigable el segundo de ellos, pues consiste en reservar el primer bit para indicar si se trata de un positivo o negativo (0 o 1) y el resto es el valor absoluto del número. No obstante, en la mayoría de ordenadores hace ya bastantes años que se emplea el primero, pues goza de dos ventajas: un mayor rango de representación posible al mismo número de bits – pues tiene una única representación para el 0 – y mayor velocidad de ejecución por parte del microprocesador de las operaciones de resta y suma. En el presente artículo, se explicará cómo funciona el complemento a dos, porqué permite realizar las operaciones aritméticas más rápidamente y porqué su resultado debe interpretarse.
En primer lugar, para entender cómo funciona, el lector debe conocer lo básico de la aritmética modular y las clases de equivalencia. En caso de que lo desconozca o bien necesite refrescarlo, al inicio de este artículo se introducen.
Los procesadores representan los números enteros en 8, 16, 32 o 64 bits dependiendo del microprocesador. Para simplificar los ejemplos inicialmente se emplearán 3 bits, que permiten representar 23 = 8 dígitos, es decir, los números comprendidos entre el 0 y el 7. Si se excede el rango, debido a la aritmética modular se sigue obteniendo un resultado, por ejemplo:
- 2 + 4 = 6 No sobrepasa el límite, el resultado es el esperado.
- 4 * 2 = 0, pues 0 ≡ 8 (mod 8)
- 4 + 5 = 1, pues 1 ≡ 9 (mod 8)
Debug en la barra de Symfony desde Twig
Este es un pequeño truco para que el volcado mediante dump() de una variable en Twig no aparezca en medio del HTML sino que lo haga en la barra de Symfony, tal y como sucede cuando el volcado se hace desde el código PHP (por ejemplo en un controlador, entidad, etc.) Curiosamente, esto no aparece en la documentación de Twig, de ahí el nombre de «truco».
Los ejemplos de uso que aparecen:
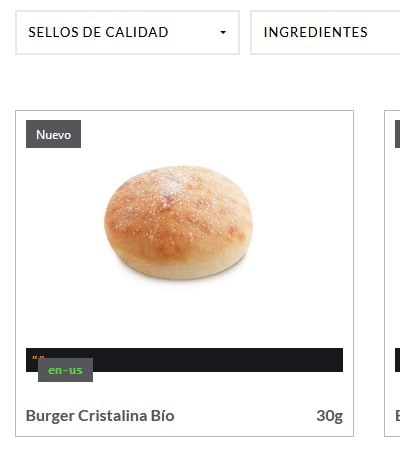
{{ dump(app.request.locale) }}
Pueden llegar a provocar un molesto resultado:
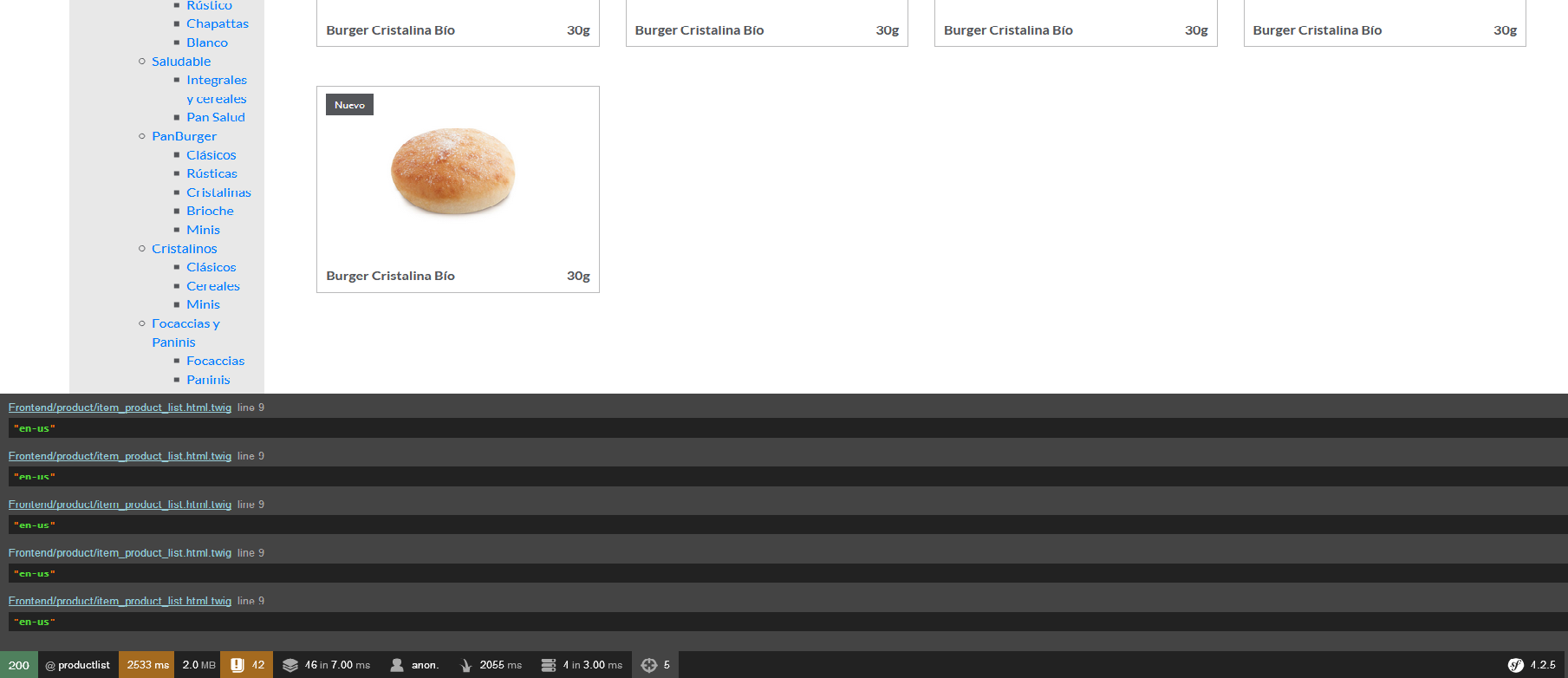
En cambio, si lo tratamos como una instrucción más mediante {% en vez de {{, el resultado se mostrará en el profiler de Symfony:
{% dump(app.request.locale) %}
Lo cual nos facilitará la vida en algunas circunstancias.
Optimizaciones inútiles del código en PHP
En las aplicaciones donde la velocidad no es determinante – categoría a la que pertenecen muchas aplicaciones web – el código, antes que optimizado, debe estar estructurado. Como los requerimientos están cambiando frecuentemente, el tiempo del programador es mucho más importante (y costoso) que el tiempo de CPU. Además, lo que puede parecernos una optimización, a veces no lo es. Veamos un ejemplo con los desplazadores de bits.
La teoría nos dice que tanto la operación de multiplicación como la de división requieren cierto tiempo de computación, especialmente esta última. Ahora bien, si esta operación se hace con una potencia de 2, se convierte en algo trivial para la CPU gracias a los desplazadores, unos sencillos bloques combinacionales formados por unas pocas puertas lógicas.
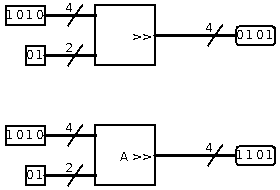
Los desplazadores tienen una señal de entrada y una de salida de n bits ambas. La señas de salida se obtiene desplazando los bits de entrada m veces hacia la derecha o hacia la izquierda El desplazamiento a la izquierda equivale a multiplicar por 2m mientras que a la derecha realiza la división entera por 2m. En el caso del desplazamiento a la derecha o división, en función del valor que se asigne a los «nuevos» bits, existen dos tipos de desplazadores:
- Lógicos: Se ponen a 0.
- Aritméticos: Se ponen al mismo valor que el bit de más peso de la entrada. Sirven para que los números codificados en complemento a dos conserven el signo.
Dos desplazadores de 4 bits: El de arriba lógico y el de abajo aritmético. Ambos desplazan 01 (2(10) bits a la derecha, i.e., dividen por 2.
Cómo simplificar una relación Many-To-Many consigo misma
En esta breve entrada expongo cómo el programador puede facilitarse un poco su actividad cuando en Doctrine establezca una relación de una entidad consigo misma. El código que se expone es de una entidad del framework Symfony, pero fácilmente se puede adaptar a cualquier entorno PHP donde, eso sí, se esté empleando este conocido ORM.
Según la documentación de Doctrine, el código para la relación Many-To-Many (de muchos a muchos) de una entidad que se referencia a si misma, por ejemplo un producto que puede tener otros productos relacionados, sería:
class Product
{
/**
* @ORM\Id()
* @ORM\GeneratedValue()
* @ORM\Column(type="integer")
*/
private $id;
/**
* @ManyToMany(targetEntity="Product", mappedBy="myProducts")
*/
private $relatedWithMe;
/**
* @ManyToMany(targetEntity="Product", inversedBy="relatedWithMe", fetch="EAGER")
* @JoinTable(name="related_products",
* joinColumns={@JoinColumn(name="product_id", referencedColumnName="id")},
* inverseJoinColumns={@JoinColumn(name="related_product_id", referencedColumnName="id")}
* )
*/
private $myProducts;
public function __construct()
{
$this->relatedWithMe = new ArrayCollection();
$this->myProducts = new ArrayCollection();
}
public function addRelatedWithMe(Product $relatedWithMe): self
{
if (!$this->relatedWithMe->contains($relatedWithMe)) {
$this->relatedWithMe[] = $relatedWithMe;
$relatedWithMe->addMyProduct($this);
}
return $this;
}
public function removeRelatedWithMe(Product $relatedWithMe): self
{
if ($this->relatedWithMe->contains($relatedWithMe)) {
$this->relatedWithMe->removeElement($relatedWithMe);
$relatedWithMe->removeMyProduct($this);
}
return $this;
}
/**
* @return Collection|Product[]
*/
public function getMyProducts(): ?Collection
{
return $this->myProducts;
}
public function addMyProduct(Product $myProduct): self
{
if (!$this->myProducts->contains($myProduct)) {
$this->myProducts[] = $myProduct;
}
return $this;
}
public function removeMyProduct(Product $myProduct): self
{
if ($this->myProducts->contains($myProduct)) {
$this->myProducts->removeElement($myProduct);
}
return $this;
}