Los ordenadores codifican internamente los números en binario. Los enteros pueden representarse mediante dos sistemas de representación: el complemento a 2 (Ca2 para abreviar) y el de signo y magnitud. Para los humanos es más amigable el segundo de ellos, pues consiste en reservar el primer bit para indicar si se trata de un positivo o negativo (0 o 1) y el resto es el valor absoluto del número. No obstante, en la mayoría de ordenadores hace ya bastantes años que se emplea el primero, pues goza de dos ventajas: un mayor rango de representación posible al mismo número de bits – pues tiene una única representación para el 0 – y mayor velocidad de ejecución por parte del microprocesador de las operaciones de resta y suma. En el presente artículo, se explicará cómo funciona el complemento a dos, porqué permite realizar las operaciones aritméticas más rápidamente y porqué su resultado debe interpretarse.

En primer lugar, para entender cómo funciona, el lector debe conocer lo básico de la aritmética modular y las clases de equivalencia. En caso de que lo desconozca o bien necesite refrescarlo, al inicio de este artículo se introducen.

Los procesadores representan los números enteros en 8, 16, 32 o 64 bits dependiendo del microprocesador. Para simplificar los ejemplos inicialmente se emplearán 3 bits, que permiten representar 2³ = 8 dígitos, es decir, los números comprendidos entre el 0 y el 7. Si se excede el rango, debido a la aritmética modular se sigue obteniendo un resultado, por ejemplo:

• 2 + 4 = 6 No sobrepasa el límite, el resultado es el esperado.
• 4 * 2 = 0, pues 0 ≡ 8 (mod 8)
• 4 + 5 = 1, pues 1 ≡ 9 (mod 8)

Como se puede observar, con este sistema cualquier número será representado en el rango [0, 7].

La siguiente operación con enteros sin signo:

6 + 7 = 5 (Pues 5 ≡ 13 (mod 8))

En la codificación en base 2 sería:

6 + 7 = 13₍₁₀ => 1101₍₂

Si se elimina este 1 inicial, el desbordamiento o overflow, el resultado es precisamente el obtenido mediante aritmética modular, pues 5₍₁₀ = 101₍₂ A continuación, veamos otra operación de suma con números diferentes que, a nivel de CPU, es exactamente igual:

-2 + (-1) = -3

Ambas operaciones, en la codificación de complemento a 2, son exactamente iguales:

110 + 111 = 1101

Es decir, en la representación en Ca2, ambos números, -3 y 5 tienen la misma representación, también la tienen los pares 6 y -2 y 7 y -1; todo depende de la «interpretación» otorgada al binario: si se considera que representa números naturales o enteros (positivos y negativos). En el siguiente esquema se representa esta situación:

 

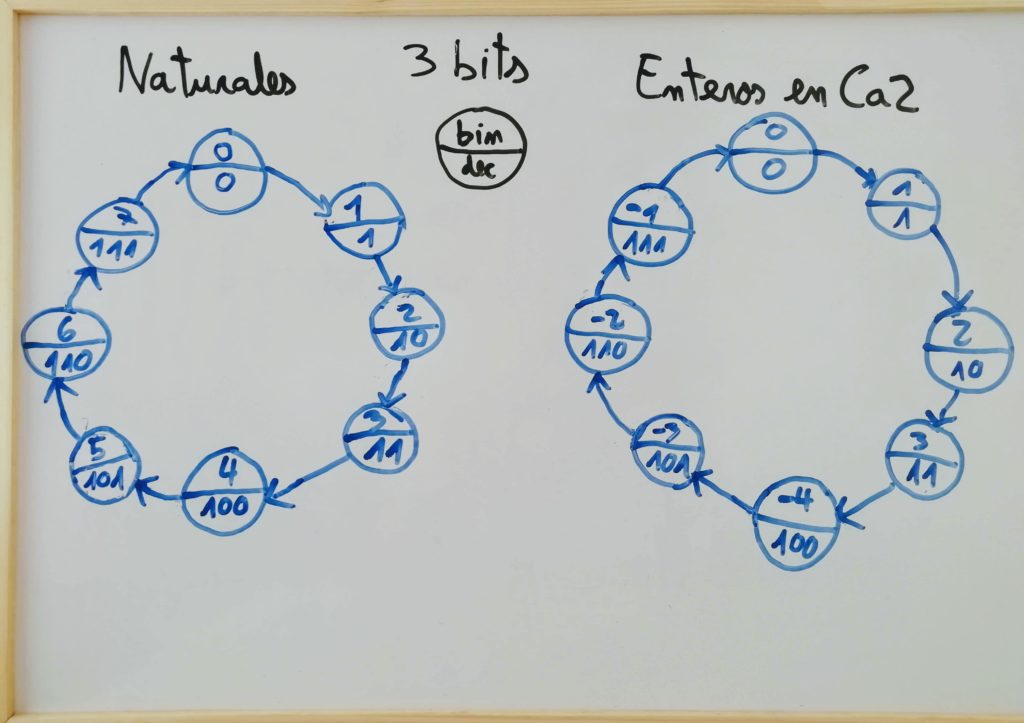
Por lo tanto, los mismos números binarios nos sirven para codificar tanto los negativos como los positivos. Es decir, a mismo número de bits, para representar sólo positivos, el rango por arriba es el doble al caso de tener que representar positivos y negativos. Concretamente, con n bits pueden representarse 2ⁿ números positivos, mientras que si se amplia a los negativos, el rango es [-2^n-1, 2^n-1 – 1]. Esto último nos permite entender porque en los lenguajes de alto nivel (por ejemplo C) se distingue entre enteros con y sin signo.

Algunos ejemplos más «realistas» con 8 bits:

100₍₁₀ = 01100100_(Ca2

90₍₁₀ = 01011010_(Ca2

01100100 + 01011010 = 10111110 = -66 = 190

-66 (mod 8) = 6 (El resto es 6 y el cociente -9 pues la condición de la división euclídea es que el resto ≥ 0, por lo que no puede ser el cociente 8 y el resto -130)

190 (mod 8) = 6

190 – 128 = 62

62 (mod 8) = 6

190 (mod 8) = 6

190 ≡ 62 ≡ -66 (mod 8)

En este caso, con 8 bits, se pueden representar números [-2^8-1, 2^8-1 – 1] = [-128, 127] o 2^8-1 si se restringe a los positivos.

Al principio del presente artículo, se comentó que este sistema de representación numérica es más rápido, veamos un ejemplo de ello para el caso de querer hallar la representación binaria de una magnitud negativa a partir de la magnitud positiva X. La representación negativa de la misma se puede obtener mediante la operación 2ⁿ – X. Ahora bien, esta no es la única forma, existen otros métodos trabajando en base 2 que son realmente rápidos a nivel de hardware, como este:

1. Se hace el complemento (de ahí el nombre de esta codificación) bit a bit, es decir, la operación booleana NOT.
2. Se suma 1.

Esta forma es también más genérica, pues cambia el signo del número, sea positivo o negativo. Existe otra forma aún más rápida:

1. Empezando por el bit menos significativo y yendo hacia el más significativo se mantienen como están hasta llegar al primer 1 (incluido).
2. A partir de aquí, se hará el complemento de cada bit restante.

En definitiva, el sistema de representación de números enteros empleado por los ordenadores modernos actuales es el complemento a 2. Los lenguajes de alto nivel sirven para aislar al programador de estos aspectos y permitirle enfocarse en la tarea a resolver, pero en momentos puntuales, tener en cuenta que hay un ordenador detrás ejecutando el programa puede ayudarle a resolverla.