Cuando estamos repasando código podemos encontrarnos expresiones booleanas en condiciones lógicas más complejas de lo necesario que dificultan entender lo que el código hace. Esto puede ser debido a que la persona no tiene los conocimientos necesarios para hacerlo mejor (en esta profesión uno se encuentra hasta biólogos sin mayor interés en la profesión que el salario) o al constreñimiento que sufrió el programador cuando desarrolló el código que estamos repasando. Por lo tanto, puede ser nuestro propio código el que incurra en esos errores que ahora, con más calma, descubrimos y nos preguntamos en qué estaríamos pensando cuando hicimos esos whiles y esos ifs.
Para reducir el total de términos de una expresión booleana existen técnicas como los mapas de Karnaugh o el método de Quine-McCluskey pero en programación generalmente es suficiente con las leyes del álgebra de Boole. Teniendo en cuenta que la condición lógica AND es el producto booleano, OR es la suma y NOT el complemento (que se puede representar con los símbolos o ¬), las leyes son:
- Idempotencia:
- x + x = x
- x * x = x
- Doble complemento:
- ¬x (doble negación) = x
- Identidad respecto a la suma y el producto o elementos neutros de la suma y del producto:
- x + 0 = x
- x * 1 = x
- Maximalidad de los elementos 1 y 0:
- x + 1 = 1
- x * 0 = 0
- Leyes asociativas respecto de la suma y del producto:
- x + (y + z) = (x + y) + z
- x * (y * z) = (x * y) * z
- Leyes distributivas respecto de la suma y del producto:
- x + y * z = (x + y) * (x +z)
- x * (y + z) = x * y + x * z
La segunda resulta familiar por ser la propiedad distributiva de la multiplicación respecto a la suma que ya conocemos del álgebra elemental. En cambio, la primera no es tan evidente pero se ve claramente su validez mediante su tabla de verdad:
| x | y | z | y*z | x + y | x + z | x + (y*z) | (x+y)* (x+z) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
- Leyes de De Morgan:
- x + y = x * y
- x * y = x + y
También las podemos comprobar mediante sus tablas de verdad:
| x | y | x | y | x+y | x+y | x*y |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
Estas leyes se pueden generalizar a más de dos variables. Además, podemos ver que x * y ≠ x*y
- Ley de absorción:
- x(x + y) = x
Su tabla de verdad es:
| x | y | x + y | x(x + y) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
La ley de absorción también se concluye aplicando las leyes anteriormente mencionadas:
x(x + y) = (x + 0)(x + y) = x + 0*y = x + 0 = x
Aplicando las leyes booleanas se deducen las siguientes propiedades:
- x + xy = x
- x + xy = x + y
- x + x = 1
- x * x = 0
Si bien las dos últimas son evidentes, para las dos primeras podemos crear sus correspondientes tablas de verdad en caso de duda.
También es conveniente conocer un teorema acerca del complemento de una función booleana y para ello hay que explicar primero qué es una función booleana. Una función booleana es algo tan sencillo como las tablas de verdad que hemos visto antes: dadas unas variables x, y, z… se obtiene un resultado F. El grado de la función es el número de variables. Este es un ejemplo de una función grado dos F2→F:
| x | y | F(x, y) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
La expresión booleana que produce tal resultado F es: x* y + x*y + x*y Aunque cómo encontrar la expresión booleana a partir de una tabla de verdad es otro tema. Ahora que ya sabemos qué es una función booleana, dejemos esta función de momento a un lado y volvamos entonces al teorema:
El complemento de una función booleana E se obtiene complementando todas sus variables e intercambiando las operaciones de suma y producto, es decir:
E(x1, x2, … xn,+,* = E(x1, x2, …,xn, *, +)
Por ejemplo el complemento de la función anterior F se podría expresar como:
F = (¬x + y) * (x + ¬y) * (x + y) = A + B + C = A + B + C = (x+y) * (x*y) * (x*y)
Con los minterm y maxterm también se acaba viendo que toda función booleana puede expresarse tanto como un conjunto de minterms multiplicados, como un conjunto de maxterms sumados. Aunque los minterm, maxterm y las formas canónicas también podrían ayudarnos, con las leyes anteriores, propiedades y el último teorema no debería haber código que se nos resista a ser simplificado. Veamos algunos ejemplos de despistes que hacen el código poco legible y como quedarían simplificados:
if (($foo && myFunction()) || ($foo && $bar)) {
Con la ley distributiva quedaría: if ($foo && (myFunction() || $bar))
if (!($foo || $bar || myFunction())) {
La expresión booleana de este if sería x + y + z
Aplicando la propiedad asociativa: x + (y + z)
Reemplazando por a: x + a
Aplicando la ley de De Morgan: x * a
Deshaciendo el reemplazo: x * (y + z)
Otra vez De Morgan: x * y * z
Así que el if original quedaría if (!$foo && !$bar && !myFunction()) {
XOR = x*y + y*x
Devuelve 1 sólo cuando x e y tienen valor diferente, o dicho de otro modo, sólo cuando una de las dos es cierta, pero no si lo son ambas. Su tabla de la verdad es:
| x | y | XOR(x, y) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Por lo tanto, el siguiente código:
if (($foo && !$bar) || (!$foo && $bar)) {
Quedaría:
if ($foo xor $bar) {
Ahora bien, si sabemos que ambas variables son booleanas, esto es exactamente lo mismo y según como hasta más legible:
if ($foo !== $bar) {
Nota:
Las leyes de álgebra de Boole están en estrecha relación con la lógica de predicados o de primer orden y con la teoría de conjuntos; esto es debido a que ambas pertenecen a este tipo de estructura algebraica. Dos ejemplos a modo ilustrativo: la ley de absorción es el modus ponens y las leyes de De Morgan también aplican a los conjuntos. Estas últimas son:
- A ∪ B = A ∩ B
- A ∩ B = A ∪ B
Veamos la segunda ley. Ésta nos dice que la intersección de todos los elementos que no son de A con la de todos los que no son de B equivale a la unión de todos los que no son de A con todos los elementos que no son de B. Su demostración es:
Una consecuencia muy interesante de las leyes de De Morgan es que AND se puede expresar mediante OR y NOT y viceversa: OR con AND y NOT. Por lo tanto, toda función booleana se puede expresar mediante una de estas combinaciones de tan solo dos condiciones lógicas. Esto se ve más claramente si se expresan en la forma de sustitución:
- x + y = ¬x * ¬y
- x * y = ¬x + ¬y
Por consiguiente, se puede crear una CPU con tan solo dos de los tres tipos de puertas lógicas capaz de ejecutar cualquier programa, por complejo que sea. Eso sí, no lograría la misma velocidad de ejecución.

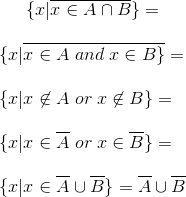
Very interesting
El asterisco de obligatorio no queda bien posicionado (se mueve)
¿Nombre y versión del navegador? ¿En móvil o en ordenador?
¡Arreglado!
Pingback: Cómo intercambiar el valor de dos variables enteras sin una intermedia | Víctor Iglesias
Pingback: Qué es una estructura de álgebra de Boole y ejemplos