Tanto en matemáticas como en informática, las funciones de orden superior son aquellas que cumplen, al menos, una de estas condiciones:
- Esperan como argumento/s una o más funciones.
- Devuelven una función como resultado.
Ejemplos en matemáticas son la derivada y la antiderivada o función primitiva.
En informática son la esencia de los lenguajes funcionales, pero también aparecen en lenguajes de otros paradigmas. Este es un ejemplo en el lenguaje Scheme en el que la función (f x) recibe un argumento y devuelve una función:
(define (f x) (lambda (y) (+ x y))) (display ((f 3) 7))
Puede ejecutarse aquí para ver el resultado.
Cuando nació Javascript, a algunos programadores les pareció un lenguaje orientado a objetos fallido1, sobretodo porque, por razones comerciales, se le puso un nombre que lo asocia con Java. Desconozco si su creador estuvo muy de acuerdo con ese nombre pues, tal y como se diseño este lenguaje, da bastante juego a la programación funcional. En el siguiente ejemplo, el método filter() es una función de orden superior, pues espera recibir una función como parámetro:
function isPrime(x){
if (x === 2) {
return true;
}
let test = x%2 !== 0;
let i = 3;
stop = Math.floor(Math.sqrt(x)); // Raíz entera de x
while (test && i <= stop) {
test = x%i !== 0;
i = i + 2;
}
return test;
}
const numbers = [47, 139, 137, 213, 2, 3, 45, 1515];
const primeNumbers = numbers.filter(isPrime);
console.log(primeNumbers);
Lo que este programa hace es filtrar la formación de números naturales «numbers«, dejando sólo los que sean primos en «primeNumbers«. Cada elemento de «numbers» será evaluado por la función «isPrime» mediante la criba de Eratóstenes. El lector puede ejecutarlo accediendo a la consola del navegador pulsando F12 y modificar el valor de «numbers» con los números (o el número) que quiera saber si son primos o no.
Este tipo de funciones están en prácticamente todos los lenguajes modernos, incluso en los que no se tuvo en cuenta el paradigma funcional en el momento de su creación. Es el caso de PHP, donde podemos encontrar una gran cantidad de funciones que esperan otra función, como es el caso de, por ejemplo, preg_replace_callback()2:
$capitalice = function($coincidencia) {
return strtoupper($coincidencia[1]);
};
echo preg_replace_callback('~-([a-z])~', $capitalice, 'hola-mundo');
Además de usar las implementadas en funciones y métodos propios del lenguaje, también podemos crear las nuestras, de forma parecida a un lenguaje completamente funcional. En Javascript, la Wikipedia nos ofrece el siguiente ejemplo:
const twice = (f, v) => f(f(v)); const add3 = v => v + 3; console.log(twice(add3, 7));
Lo mismo es posible en PHP:
$twice = function($f, $v) {
return $f($f($v));
};
$f = function($v) {
return $v + 3;
};
echo($twice($f, 7));
La programación funcional pretende tratar la programación como la evaluación de funciones matemáticas, paradigma muy diferente a la programación imperativa, basada en estados y en instrucciones que lo cambian. Tal vez las características funcionales que tienen algunos lenguajes puedan ayudarnos a introducirnos en un paradigma, el funcional, que nos exige una forma muy distinta de enfocar los problemas.
1 Todavía hoy en día, y a pesar de los cambios que ha sufrido en los últimos ECMA, sigue despertando las críticas de los programadores que, debido a su nombre, esperan que se comporte como un lenguaje completamente orientado a objetos, como Java, y se dan de bruces contra la realidad.
2 El parámetro que recibe la función contenida en $capitalize son las coincidencias que encuentre la expresión regular.
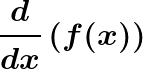
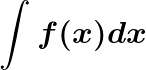
Los operadore funcionales lineales S() (antiderivada) y D() (derivada) dotan a los conjuntos de funciones derivables en un punto y funciones integrables en un intervalo de estructura de espacio vectorial ya que:
S(f+g)=S(f)+S(g) y S(aF)=aS(f)
D(f+g)=D(f)+D(g) y D(af)=aD(f)
El axioma de la elección:
https://es.wikipedia.org/wiki/Axioma_de_elecci%C3%B3n
nos asegura que todo espacio vectorial admite una base, y por tanto una dimensión. Una pregunta interesante es localizar bases de los anteriores e.v. y saber cual es su dimensión.
Como curiosidad el matemático que descubrió i estudió la Geomatria Integral fué el matemático catalán Ferran Sunyer i Balaguer
https://ca.wikipedia.org/wiki/Ferran_Sunyer_i_Balaguer
Por último, el operador derivada da origen a la Geometría Diferencial, una de las ramas más importantes de la matemáticas
Algo que me llamó la atención en su momento es dotar de una estructura de espacio vectorial a objetos que no son vectores, pues, según la primera definición que conocí, los elementos de un espacio vectorial son vectores. Por ejemplo, el conjunto de los polinomios forma un espacio vectorial, pero los polinomios no son vectores. O en el caso que comentas, las funciones no son vectores.
Otro ejemplo de la confusión son las aplicaciones lineales (por ejemplo la de escalado) donde los «vectores» que se van a multiplicar por la matriz de escala realmente son las coordenadas de un punto, no un vector.
La palabra vector se suele reservar para los espacios vectoriales basados en R^n, en los cuales tiene sentido asignar a cada vector una dirección, un sentido y una intensidad (o módulo). En el resto de e.v. sus elementos suelen conservar su nombre (no tiene mucho sentido llamar vector a un polinomio).
Esta mañana he publicado un artículo sobre este tema que hacía unos meses que tenía en la lista de artículos pendientes:
https://www.victoriglesias.net/generalizacion-de-los-espacios-vectoriales/
Inicialmente, tenía pensado poner sólo el ejemplo de los polinomios, pero he añadido también las funciones reales a los ejemplos de objetos matemáticos que pueden tratarse como espacios vectoriales.