En este tercer y último artículo contesto la pregunta con la que finalizaba el segundo: ¿cómo calcular la exponenciación de un número real a uno complejo?
Si tenemos en cuenta que para cualquier número real, a, se cumple que a = eln(a), por la misma definición de logaritmo, tenemos:
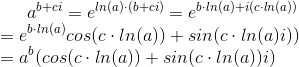 Hasta ahora, en todos los casos que hemos visto, la base era e, y en este artículo hemos generalizado a cualquier base real. Generalizando aun más, para a y b reales1 o complejos, la operación exponenciación, ab , puede calcularse mediante la operación:
Hasta ahora, en todos los casos que hemos visto, la base era e, y en este artículo hemos generalizado a cualquier base real. Generalizando aun más, para a y b reales1 o complejos, la operación exponenciación, ab , puede calcularse mediante la operación:
1 Si a ∈ ℝ, a > 0
Como anécdota, y desviándome de la temática de estos tres artículos, está el hecho de que a partir de la igualdad a = eln(a) se deduce la derivada de las funciones exponenciales de base a que en el Bachillerato tuvimos que memorizar, pero veamos de dónde viene: ![]() Por la regla de la cadena, tenemos que la función exterior f(x) es ex, mientras que la interior g(x) es ln(a)x, cuya derivada g'(x) = ln(a) pues podemos y debemos ver ln(a) como un número real cualquiera. Por lo tanto, la derivada es:
Por la regla de la cadena, tenemos que la función exterior f(x) es ex, mientras que la interior g(x) es ln(a)x, cuya derivada g'(x) = ln(a) pues podemos y debemos ver ln(a) como un número real cualquiera. Por lo tanto, la derivada es:
![]() La parte derecha de la ecuación es ax pues habíamos establecido que a = eln(a), por lo que finalmente tenemos la receta que nos dieron para memorizar:
La parte derecha de la ecuación es ax pues habíamos establecido que a = eln(a), por lo que finalmente tenemos la receta que nos dieron para memorizar:
![]() La receta para calcular la integral también la podemos deducir con la la misma igualdad.
La receta para calcular la integral también la podemos deducir con la la misma igualdad.
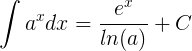
Pingback: i elevado a i | Víctor Iglesias
Por fa ir me puede dar el resultado, según lo explicado, ¿ Cuáll es el resultado de 1Exp(1+1i) ,
Bien, no explicas nada pero todo correcto. Mil gracias por decir que lo que es así es así.
Sí que explica. Ha dicho cómo se calcula una potencia con exponente complejo basándose en las propiedades de los logaritmos. Llevo días buscando una explicación así en internet y por fin la he encontrado. Muchas gracias.
1+0i = 1