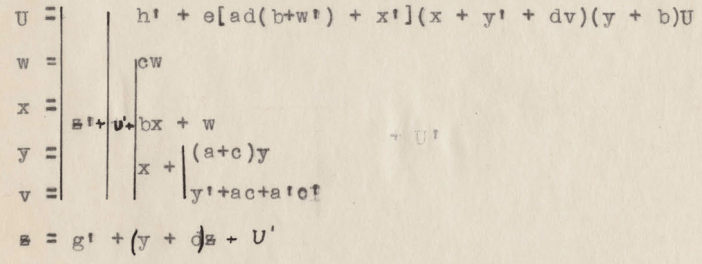Alguien o algunas personas, en algún momento de principios del siglo XX, pensó que para crear una máquina que realizara ciertos cálculos, podría ser conveniente emplear la electricidad, las puertas lógicas, usar la base 2 como sistema de numeración y el álgebra de Boole, es decir, alguien debió sentar las bases técnicas del ordenador moderno. Personalmente, siempre tuve la duda de cómo fue ese proceso. Si bien es bastante conocido que el primer diseño de un ordenador digital fue realizado por Von Neumann en los años 40 y que los ordenadores actuales se basan en el mismo, resulta evidente que entre la máquina analítica de Charles Babbage (mecánica y que operaba en base 10) y Von Neumann debieron pasar bastantes cosas.
Bastantes años atrás, leí que Von Neumann dio una respuesta afirmativa a la pregunta de si la creación de su ordenador estaba influenciada por el trabajo de Alan Turing de 1936, en el que presenta el concepto de lo que ahora se conoce como «máquina de Turing» para resolver el problema matemático de la decibilidad. No obstante, el trabajo del matemático inglés es puramente conceptual y está centrado en resolver este célebre problema de lógica matemática, y no dice nada acerca de la base física o ingenieril de una máquina de Turing.
Recientemente he podido descubrir quién fue el creador de esta parte y cómo fue ese proceso. La clave está en la tesis de máster de Claude Elwood Shannon de 1937 llamada «A symbolic analysis of relay and switching circuits«. No la conocía y resulta que está considerada «una de las tesis de máster más importantes jamás escrita». Sus 69 páginas no tienen desperdicio, me han dado las respuestas que buscaba. En primer lugar, se entiende cuál era la situación del momento: ya existían circuitos para automatizar operaciones más o menos complejas, como centralitas de telefonía o equipos de control de motores industriales. Estos circuitos se fabricaban con relés y selectores rotativos. Este vídeo describe muy bien cómo funciona un relé:
En su tesis el autor identifica dos problemas en el trabajo con estos circuitos:
- El análisis de los mismos, es decir, determinar qué hace un circuito ya existente.
- La síntesis: consiste en crear un circuito a partir de unos requerimientos. La solución no es única y debería encontrarse la que requiere menor número de componentes.
La solución que el autor propone para ambos problemas es representar cada circuito mediante un conjunto de ecuaciones, cuyos términos representan los relés e interruptores del circuito. Para manipular las ecuaciones, Shannon desarrolla lo que denomina un «cálculo» (calculus), y demuestra que éste es análogo al «cálculo» de lógica proposicional (hoy en día simplemente se denomina «lógica de enunciados»). A continuación, expone que el álgebra de Boole es aplicable. Esto es debido a que la lógica de enunciados tiene estructura de álgebra de Boole.
Shannon no sigue la convención actual, él emplea el 0 para representar un circuito abierto (pasa corriente) y el 1 para el circuito cerrado (no pasa corriente), esto es importante tenerlo en cuenta para entender las primeras páginas. La suma u OR lógico se consigue mediante dos contactos ubicados en línea, accionado cada uno por un relé, mientras que el producto o AND lógico mediante dos interruptores en paralelo:

El lado izquierdo del signo igual es una representación algo más «realista», mientras que el lado derecho es una abstracción simbólica.
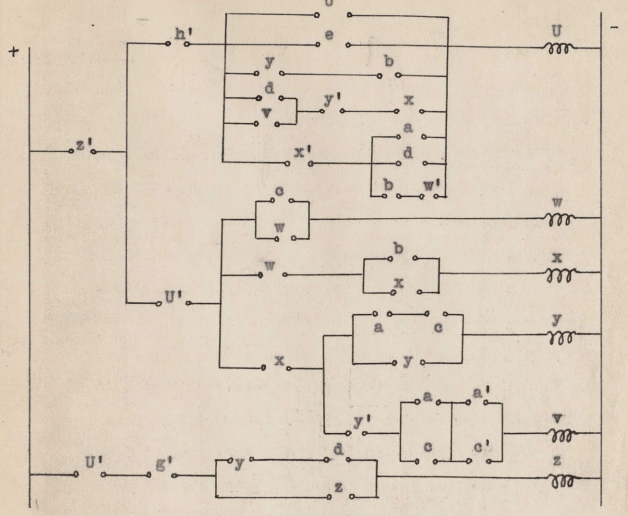
En los siguientes esquemas se representa de forma un poco más detallada cómo crear las puertas lógicas AND y OR con humildes relés:

Puerta lógica OR

Puerta lógica AND
Si bien ambos diseños se podrían simplificar para emplear un único relé, éstos son de una mayor claridad. Por cierto, la puerta lógica NOT se puede implementar con un relé inverso (en el vídeo también se explica en qué consiste este relé).
En su tesis, después de desarrollar los conceptos básicos, explicar la analogía con la lógica de enunciados, mostrar los teoremas de álgebra de Boole que serán útiles para la síntesis de circuitos y poner ejemplos prácticos de su aplicación, en las páginas 16 / 17 hace una afirmación que parece avanzada a su tiempo:
También es posible emplear la analogía entre el álgebra de Boole y los circuitos de relés en dirección contraria, es decir, representar relaciones lógicas mediante circuitos eléctricos. Siguiendo esta línea se han obtenido algunos resultados interesantes, pero no son de importancia aquí.
Al decir que los circuitos pueden hacer cálculos lógicos, ha concebido el ordenador digital moderno. Su afirmación de que esto carece de importancia en su tesis no sé si es por modestia o porque no intuye sus disruptivas aplicaciones futuras. Al final de su tesis muestra el diseño de dos máquinas: una es un «sumador eléctrico» (electric adder) que trabaja en base 2 y la otra da todos los múltiplos de todos los primos menores o iguales a 10.000, a partir de la cual un humano sabrá que cualquier número inferior a 100.000.000 que no esté en la lista obtenida es un número primo (aunque la del diagrama de ejemplo está limitada a los tres primeros primos). Hasta el momento, hacer una lista así manualmente había representado un gran esfuerzo y encima con algunos errores, como Shannon explica. Si bien estas máquinas parecen ordenadores primitivos, todavía les falta una memoria programable, además de carecer de condicionales y saltos.
En definitiva, esta tesis sentó las bases para la creación de circuitos digitales (y por lo tanto de los ordenadores) con una base teórica sólida, a diferencia de cómo se diseñaban los circuitos en esa época y mucho antes de la invención del transistor. Si bien este no es el trabajo más famoso de Claude Elwood Shannon, fue fundamental para sentar las bases del fenómeno que más ha cambiado la existencia del ser humano durante la segunda mitad del siglo pasado y del actual. En lo personal, descubrirlo ha sido encontrar mi eslabón perdido entre por un lado Babbage y por el otro Von Neumann y la tesis de Church-Turing.