En la EGB nos podrían haber explicado mejor las matemáticas, me di cuenta de esto años después, en Bachillerato, y a las malas. Si no es tu caso, me alegro por ti; en el nuestro tuvimos profesores que no tenían claro lo que explicaban, no se trataba de saber mucho (es sólo la EGB) sino de tenerlo muy claro. En mi opinión, en matemáticas es preferible avanzar poco pero con firmeza a avanzar mucho sin solidificar las bases, lo que conduce más pronto que tarde al desmoronamiento de lo que creíamos saber.
A continuación, expondré cómo me parece que hubiera sido mejor que explicaran algunos aspectos. Si eres profesor, espero que te pueda servir mi opinión (puedes dejarme la tuya en los comentarios); si eres alumno de la educación obligatoria, tal vez esto puedo ayudarte a clarificar algunos conceptos.
Los miembros de una ecuación no «pasan» al otro lado
Recuerdo que el profesor usaba expresiones como:
- x pasa a dividir (o a multiplicar) al otro lado.
- Tal número pasa a restar (o a sumar) al otro lado.
Como ejemplo de los errores a los que puede conducir pensar así, veamos la ecuación de la división entera, donde D es el dividendo, d el divisor, q el cociente y r, r≥0, el residuo:
D = d*q + r
Si pensamos que D «pasa a dividir al otro lado», como el lado izquierdo de la igualdad queda vacío, podemos creer que esto es correcto:
0 = (d*q + r) / D
Si nos hubieran enseñado que, como ambos lados de la ecuación son iguales, la igualdad se mantendrá si operamos igual en ambos lados, pensaremos que vamos a dividir a ambos lados por D, con lo que llegaremos a una igualdad correcta:
D/D = (d*q + r) / D → 1 = (d*q + r) / D
Segmentar la resolución de una ecuación
Otra zancadilla en nuestro aprendizaje nos la daba un profesor que usaba el punto y coma «;» para separar cada paso que ejecutaba para resolver la ecuación. Arrastré la coletilla hasta que en el Bachillerato, un compañero me preguntó por qué usaba un punto y coma en vez del signo igual. Tal vez sería más pedagógico usar el símbolo «implica que»:
x2 -9 = 0 ; x2 = 9 ; x = √3; x = ±3
x2 -9 = 0 ⇒ x2 = 9 ⇒ x = √3 ⇒ x = ±3
Lo que implica la igualdad
Deberían habernos dejado bien claro, incluso diría que machacado, que el hecho de que los dos lados de la ecuación sean iguales implica que seguirán siéndolo si se realiza la misma operación en ambos lados: elevar al cuadrado, al cubo, raíz cuadrada a ambos lados, etc. Cuando llega el momento, no está de más explicar que operaciones como las raíces pueden tener la limitación x ≥ 0 cuando operamos ecuaciones que las contienen, por ejemplo:
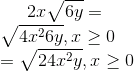
Estas condiciones son frecuentes en matemáticas: aparecen en los logaritmos y, pasada la educación obligatoria, vuelven a aparecer en el cálculo de límites, en las integrales, etc.
Potencia con exponente
En matemáticas se tiende a obviar los paréntesis que no son imprescindibles, esto nos puede inducir a creer que la siguiente igualdad es cierta, cuando no lo es:
![]() En este caso, por la prioridad de los operadores, primero debe calcularse 34, 81, para finalmente operar 281. En cambio, mediante los paréntesis podemos indicar que la base no es 2 sino 23, es decir, la potencia de una potencia:
En este caso, por la prioridad de los operadores, primero debe calcularse 34, 81, para finalmente operar 281. En cambio, mediante los paréntesis podemos indicar que la base no es 2 sino 23, es decir, la potencia de una potencia:
Simplificaciones incorrectas
En el trabajo de una expresión matemática nunca puede irse en «piloto automático» sino que hay que tener muy claro en cada paso lo que se está haciendo. Esto es fundamental en el aprendizaje de las matemáticas.
Consecuencia del ejemplo anterior con la raíz, la siguiente simplificación, en algunas circunstancias, es falsa:
√x² ≠ x
La correcta es:
√x²= |x|
Cuando nos dan la fórmula de la ecuación de segundo grado, aparece el ± acompañando la raíz del radicando. Pues bien, cuando unas clases más adelante se explica que un elemento al cuadrado dentro de una raíz se simplifica, se debería dejar muy claro que, por convención, √x hace referencia a la solución positiva, mientras que -√x se refiere a la negativa. Por ejemplo:
√9 = 3
-√9 = -3
En el caso del cuadrado dentro de la raíz, sería:
√3² = 3
No obstante, en el caso de la raíz positiva, se produce una ambigüedad que se solventa mediante el empleo del valor absoluto. Esta ambigüedad surge porque se obtienen resultados diferentes dependiendo de si se elimina primero la raíz o se calcula primero la potencia:
Gracias al valor absoluto, se aclara que sólo se hace referencia la solución positiva, √ en vez de -√. Como anécdota, decir que obviar esto conduce a una demostración según la cual 2 + 2 = 5.
Esta otra trampa de simplificación es algo más sutil, partiendo del hecho que:
![]() Es decir, el resultado no es x³, podemos caer en el siguiente error:
Es decir, el resultado no es x³, podemos caer en el siguiente error:
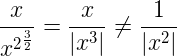 La no igualdad sólo se convertiría en igualdad para los casos x > 0. Ahora bien, si sí o sí es necesario sacar la x del numerador, esta simplificación también es correcta:
La no igualdad sólo se convertiría en igualdad para los casos x > 0. Ahora bien, si sí o sí es necesario sacar la x del numerador, esta simplificación también es correcta:
La proporcionalidad
Acerca de las fracciones nos enseñaron prácticamente todo, pero viéndolo desde la distancia, me parece que se pasó a la ligera por el hecho de que el cociente entre dos magnitudes expresa cuánto de la magnitud del numerador corresponde a cada unidad de la magnitud del denominador. Después, en el Bachillerato, esto aparece de forma masiva en asignaturas como Química y Física:
- F/m: La aceleración es la fuerza que actúa por unidad de masa.
- F/q: La intensidad del campo eléctrico es la fuerza que actúa por unidad de carga eléctrica.
- d = m/V: La densidad es la masa de un objeto por unidad de volumen.
En el cotidiano acto de la compra tenían nuestros profesores un buen ejemplo, si por ejemplo un cartel anuncia que la malla de 6 Kg de naranjas cuesta 3’84€ y queremos saber cuánto cuesta el kilogramo, tendremos que poner el precio en el numerador y el peso en el denominador, pues deseamos conocer el precio en función del peso.
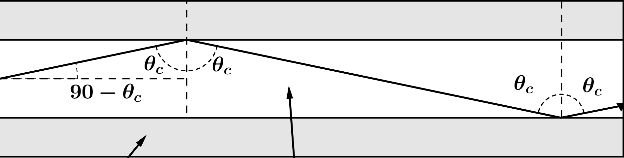
Aunque el ejemplo de la compra pueda parecer muy básico, el mismo concepto, la proporcionalidad, permite hallar la solución a problemas aparentemente más complejos, como el siguiente que nos servirá a modo de ejemplo. Tenemos un tramo de fibra óptica de 300 metros por el que se desplaza un haz de luz (línea negra), «rebotando» por reflexión total interna.
Si sólo sabemos el valor de ϴc como la luz no se desplaza en línea recta sino en zigzag, aparentemente no podemos calcular la distancia real que recorre la luz, pero gracias a la proporcionalidad directa y algo de trigonometría podemos encontrar solución.
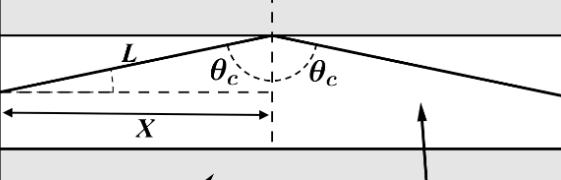
![]() Vemos que existe una proporcionalidad directa entre X y L, pues sen(ϴc) es una constante. Es decir, si en 300 metros caben n segmentos X, habrá el mismo número de segmentos L, n ∈ ℝ+. Como:
Vemos que existe una proporcionalidad directa entre X y L, pues sen(ϴc) es una constante. Es decir, si en 300 metros caben n segmentos X, habrá el mismo número de segmentos L, n ∈ ℝ+. Como: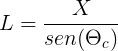 Si llamamos e a la distancia real recorrida por luz, sabemos que la siguiente igualdad, que nos permite calcular la distancia realmente recorrida en zigzag, es cierta:
Si llamamos e a la distancia real recorrida por luz, sabemos que la siguiente igualdad, que nos permite calcular la distancia realmente recorrida en zigzag, es cierta:
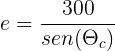 En definitiva, creo que una mayor dedicación y rigurosidad en la exposición de los conceptos básicos nos hubiera ayudado a aposentar los cimientos de las matemáticas; una asignatura difícil, incluso para enseñarla.
En definitiva, creo que una mayor dedicación y rigurosidad en la exposición de los conceptos básicos nos hubiera ayudado a aposentar los cimientos de las matemáticas; una asignatura difícil, incluso para enseñarla.
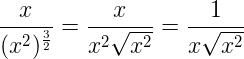
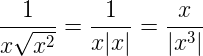
Muy cierto, lo de «pasar al otro lado» induce a errores del tipo 6=3x+2; 6/3=x+2; x=0. Lo del ; se puede admitir para separar los distintos pasos en la resolución de la ecuación. Lo más correcto sería la doble implicación
El error que comentas, además de ser debido a la confusión que genera el «pasar al otro lado», como indicas, tal vez también es debido a no explicar claramente qué significa que una expresión algebraica es igual a otra, pues en el ejemplo que pones se esta cogiendo una parte (x) por el todo(x + 2)
Hola Víctor.
En mi humilde opinión, las matemáticas se han explicado y continuan explicándose mal, desde el principio, desde la primera toma de contacto con ellas.
Se obvia completamente la realidad de las inteligencias múltiples, los diferentes ritmos y estilos de aprendizaje, la idiosincrasia de cada estudiante, y otras muchas variables. El aprendizaje significativo, el saber y conocer la realidad, la naturaleza de los diferentes objetos matemáticos y las diferentes relaciones e interacciones entre ellos, carece de la menor importancia. Sólo cuenta la respuesta mecanizada, la buena memoria procedimental; repetir, repetir y repetir hasta dominar el ejerecicio.
Por no hablar de los profesores que dan la sensación de no conocer la materia. Explicaciones tomadas literalmente de los libros de texto, respuestas que nada aclaran, muchos dogmas de fé disfrazados de axiomas, tautologías por doquier y demostraciones que casi nada demuestran, pues el alumno no comprende la lógica ni el proceso de las mismas. Y, como no, las prisas, presiones, la urgencia y exigencia por parte de las autoridades educativas, para que los docentes completen el programa de la asignatura.
No creo que sea necesario decir que mi experiencia con las matemáticas fué, y es, desastrosa. Por todo lo anteriormente comentado, y por limitaciones propias en el manejo de contenidos abstractos, mi comprensión de lo numérico debe ser equiparable a la de un niño de cuarto de primaria, y no veo perspectivas de mejora.
El nivel de exigencia actual, que obliga a cualquier estudiante a adquirir un conocimiento en matemáticas equivalente al del segundo de bachillerato( 2º de BUP) de mi época, es claramente exagerado, inalcanzable para la gran mayoría de jóvenes. Si tuviese poder e infuencia para ello, propondría varias medidas para intentar paliar parte de la problemática educativa actual.
En lo referente a las matemáticas, que es lo que nos ocupa; cambio total, radical, de la metodología didáctico-pedagogica, priorizando el aprendizaje manipulativo y significativo de la materia.
Creación de itinerarios diferenciados atendiendo a las inteligencias múltiples; teniendo en cuenta los intereses, habilidades y preferencias de los estudiantes.
Implementación de un nivel de matemáticas básico, centrado en la comprensión y manejo de los números naturales y las diferentes operaciones con los mismos.Introducción, visión filosófica e histórica del desarrollo y descubrimiento de los diferentes objetos y herramientas matemáticas. A medida que el estudiante avanza, se introducirían conceptos tales como la estimación y manejo de las cantidades fraccionarias usadas comúnmente, cálculo de porcentajes, planteamientos de problemas relacionados con usos reales y cotidianos, cálculo mental, etc. En cursos como 3º y 4º de ESO, introducción a la lectura, interpretación y manejo de diferentes documentos como facturas, extractos bancarios, formularios de declaración de la renta, etc;con las limitaciones y adaptaciones necesarias para adecuarlas a las posibilidades de los estudiantes…
Se seguiría ofreciendo, para aquellos alumnos capaces de manejarlas y que libremente las elijan, matemáticas de niveles más avanzados.
Estas son algunas de mis ideas y reflexiones. Gracias por permitirme compartirlas.
Un saludo
Hola Juan,
En primer lugar, gracias por tu comentario, no es frecuente encontrar opiniones tan bien razonadas como la tuya.
En segundo lugar, decirte que estoy muy de acuerdo con tu opinión. Como tú bien dices, hay mucha presión por avanzar temario. En mi humilde opinión, teniendo en cuenta que el máximo responsable de los temarios es el Ministerio de Educación, una posible razón por la que se desea que los alumnos avancen, aunque sea enseñando a los alumnos a memorizar recetas para la resolución de problemas matemáticos, es que el país obtenga la mejor puntuación posible en las pruebas PISA. Así, el partido político que hizo la enésima reforma educativa, puede defenderla delante del electorado.
Actualmente, por ejemplo, es perfectamente posible que un alumno de bachillerato calcule correctamente la velocidad instantánea derivando la posición respecto al tiempo pero falle el problema por no saber aplicar correctamente la proporcionalidad. No es realista creer que con tres horas semanales de física y otras tres de matemáticas, vamos a tener bachilleres capaces de realmente entender conceptos que necesitaron siglos de gestación.
Ojalá se dedicaran a la educación suficientes recursos para poder explicar las matemáticas como es debido y, además, con diferentes itinerarios según las inclinaciones de los niños. Recursos el país los tiene, otra cosa es la voluntad de los políticos, los ciudadanos que los votamos, los profesores y, como no, los propios alumnos y sus padres.
Un saludo.
Hola de nuevo, Víctor.
Estoy de acuerdo contigo; todo parece indicar que se presiona a docentes y estudiantes, obligándoles a completar los temarios de algunas asignaturas, matemáticas en el caso que nos ocupa, para obtener buenas puntuaciones en las pruebas PISA.
Movido por la curiosidad, he averiguado que las famosas pruebas (realizadas por encargo de la OCDE, una plataforma interestatal para la potenciación y fomento de la economía de mercado) son creadas y corregidas por una empresa privada llamada Pearsons, una editorial británica especializada en libros de texto; multinacional propietaria, entre otros medios, del archiconocido Financial Times. Ellos diagnostican los «males» del sistema educativo y te venden las «medicinas» en formato libro de texto. Negocio redondo. Todo muy sospechoso como mínimo…Mercantilización de la enseñanza en su máxima expresión. Respecto al ministerio de educación, gobierno , gobernantes y demás, prefiero no hacer comentarios.
Por otra parte, la enseñanza de las matemáticas, con su naturaleza tan particular, lo complejo e inaccesible para las masas, y en particular para mí, de muchos de sus conceptos, requiere un cambio completo de enfoque y rumbo. No hace falta llegar al asunto de las derivadas, como ponías de ejemplo en tu respuesta a mi comentario. Quienes tenemos grandes dificultades con la materia, tropezamos mucho, muchísimo antes. No tengo ninguna idea, ni sugerencias de soluciones para este asunto; tan sólo puedo plantear ciertas cuestiones o reflexiones en voz alta:
¿Sinceramente, tú crees que la idea de número negativo es accesible y comprensible para la mayoría de estudiantes?. Para mí, que tengo 46 años, no lo es. ¿ Crees que se conoce el significado de las operaciones con fracciones?. ¿Para que operar con polinomios?. ¿Por qué se mantiene en el programa de estudios los logaritmos si no se enseña al estudiante la naturaleza, origen y características de los mismos (que no es lo mismo que sus propiedades)?. Como bien dices, si el desarrollo de ciertas herramientas matemáticas necesitó siglos de trabajo por parte de mentes excepcionales como Newton o Leibniz, ¿es razonable que jóvenes adolescentes se enfrenten en tan sólo uno o dos cursos de bachiller al cálculo diferencial y toda su complejidad conceptual?. Más aún si se tiene en cuenta que hasta los 20 años, no está completamente desarrollada y madura el area cerebral que permite asimilar los conceptos abstractos. Y así , centenares de preguntas más.
Gracias.
Un saludo.
Hola Juan,
Muy interesante sobre las pruebas PISA, aquí está el link donde la misma Pearson anuncia que ha ganado la licitación:
http://www.pearsoneducacion.net/colombia/noticias/2018/04/30/blank
Un saludo.