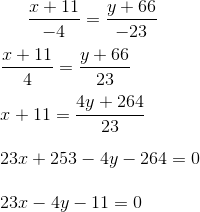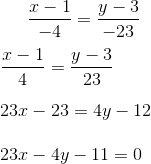En el artículo anterior expliqué cómo se resuelven las ecuaciones diofánticas y su relación con las ecuaciones de congruencia. En la presente entrada vamos a ver un programa en Python que las resuelve.

#! /usr/bin/env python
# -*- coding: utf-8 -*-
# Resuelve ecuaciones diofánticas tipo ax + by = c

import sys
from sys import argv

def extendedEuclideanAlgorithm(old_r, r):
    negative = False
    s, old_t = 0, 0
    old_s, t = 1, 1

    if (r < 0):
        r = abs(r)
        negative = True
        
    while r > 0:
        q = old_r / r
        #MCD:
        r, old_r = old_r - q * r, r
        #Coeficiente s:
        s, old_s = old_s - q * s, s
        #Coeficiente t:
        t, old_t = old_t - q * t, t
        
    if negative:
        old_t = old_t * -1
        
    return old_r, old_s, old_t

a = long(argv[1])
b = long(argv[2])
c = long(argv[3])

mcd, s, t = extendedEuclideanAlgorithm(a, b)
if c % mcd == 0:
    a1, b1, c1 = -a / mcd, b / mcd, c / mcd
    x1, y1 = s * c1, t * c1
    print "x = {0}{1:+d}k" . format(x1, b1)
    print "y = {0}{1:+d}k" . format(y1, a1)
else:
    print "No tiene solución"

Para calcuar 23x -4y = 11 hacemos:

vic@LESBIAN:~/mates$ ./diofanticas.py 23 -4 11
x = -11-4k
y = -66-23k

Aplicando el concepto de clase de equivalencia, tal y como se explica en el anterior artículo, podemos computar la forma paramétrica más simplificada como muestra el siguiente programa:

#! /usr/bin/env python
# -*- coding: utf-8 -*-
# Resuelve ecuaciones diofánticas tipo ax + by = c
# El primero par x e y es la forma parmétrica más simplificada
 
import sys
from sys import argv

def extendedEuclideanAlgorithm(old_r, r):
    negative = False
    s, old_t = 0, 0
    old_s, t = 1, 1

if (r < 0):
    r = abs(r)
    negative = True

while r > 0:
    q = old_r / r
    #MCD:
    r, old_r = old_r - q * r, r
    #Coeficiente s:
    s, old_s = old_s - q * s, s
    #Coeficiente t:
    t, old_t = old_t - q * t, t

if negative:
    old_t = old_t * -1

return old_r, old_s, old_t

a = long(argv[1])
b = long(argv[2])
c = long(argv[3])

mcd, s, t = extendedEuclideanAlgorithm(a, b)
if c % mcd == 0:
    a1, b1, c1 = a / mcd, b / mcd, c / mcd
    x1, y1 = s * c1, t * c1
    # Uso abs() pues Python no hace la división Euclídea con cociente negativo
    equivClass = x1 % abs(b1)
    print "x = {0}{1:+d}k" . format(equivClass, b1)
    print "y = {0}{1:+d}k" . format((c1 - (a1 * equivClass)) / b1, -a1)
    print "x = {0}{1:+d}k" . format(x1, b1)
    print "y = {0}{1:+d}k" . format(y1, -a1)
else:
    print "No tiene solución"

Este es el resultado de diferentes ejecuciones:

vic@LESBIAN:~/mates$ ./diofanticas.py 4 7 29
x = 2+7k
y = 3-4k
x = 58+7k
y = -29-4k

vic@LESBIAN:~/mates$ ./diofanticas.py 23 -4 11
x = 1-4k
y = 3-23k
x = -11-4k
y = -66-23k

El uso de la función abs(), que nos devuelve el valor absoluto, es debido a que Python no hace la división Euclídea cuando el cociente es negativo. Los dos pasos:

• q = old_r / r
• old_r = old_r – q * r

Se podrían unificar con la función divmod(), pero me parece menos claro para quien no conoce el lenguaje, siendo los dos pasos más parecidos al pseudocódigo.

Editado el 11/03/2018:

Casi un año después de su publicación, observo en Google Analytics que este artículo tiene un porcentaje de rebote muy elevado. Tal vez este sea debido a que la mayoría de visitantes estén buscando simplemente un programa que resuelva congruencias lineales. Si es tu caso, para ejecutar el programa que aparece al final de esta entrada, puedes instalar fácilmente el intérprete de Python 2 en tu ordenador, es muy ligero y existe para todas las plataformas. Como alternativa, dispones de intérpretes en línea (1, 2) donde puedes copiar y pegar el código; después deberás modificarlo ligeramente porque los parámetros no serán argumentos pasados a través de la línea de comandos.

Una ecuación de congruencia es una congruencia entre expresiones literales, los valores que la satisfacen son sus soluciones. Por ejemplo 13x ≡ 5 (mod 77) es una ecuación de congruencia.

Sus soluciones nos las da x ≡ 30 (mod 77) Es decir, todos los infinitos x que al dividirlos por 77 dan el mismo resto que 30/77 Dicho resto es 30 y todos los x serían múltiplos de 77^· + 30: 30, 107, 184, 261…

Si reemplazamos estos x en la ecuación de congruencia lineal inicial veremos que son soluciones:

13*30 ≡ 30 (mod 77) => Resto 5. Así como dan el mismo resto:

13*107 ≡ 30 (mod 77)

13*184 ≡ 30 (mod 77)

…

Para poder encontrar la solución de una congruencia lineal en primer lugar hay que saber hallar el inverso de a (mod m) Este inverso, a’, es un número tal que a’*a ≡ 1 (mod m)

Por ejemplo, el inverso de 6 (mod 11) es 2: 2*6 ≡ 1 (mod 11)

Teorema: La condición necesaria y suficiente para que dos números a y b sean congruentes respecto al módulo m es que su diferencia sea un múltiplo de m, es decir, m | (a -b)

Por lo tanto en el ejemplo sería 11 | (a’ * 6 – 1) => 6a’ – 1 = 11^· , 6a’ = 11^· + 1 Como ha de ser un múltiple de 11 + 1 vemos fácilmente que a’ = 2 cumple la condición.

Si para hallar el inverso de 2 (mod 8) hacemos: 8 | (a’ * 2 – 1) Vemos que no hay solución pues 2a’ -1 siempre será un número impar mientras que 8 es par. Por lo tanto no siempre existe un inverso. El siguiente teorema nos permite saber cuando existe el inverso:

La condición necesaria y suficiente para que un entero a posea un inverso módulo m, m > 1, es que mcd(a, m) = 1 Además, si existe tal inverso, ese inverso es único módulo m.

Esto nos resulta familiar con el teorema de Bezout explicado en el artículo anterior. Por ejemplo, para calcular el inverso de 111 (mod 250) primero calculamos mcd(111, 250) = 1 Por lo tanto sabemos que existe un inverso a’ y que habrá un s y un t tal que:

111 *s + 250 * t = 1

Aplicando el algoritmo del artículo obtenemos s = -9 y t = 11 y por lo tanto a’ = -9. Así es:

-9 * 111 ≡ 1 (mod 250)

• -999 dividido entre 250 da el mismo resto que 1 entre 250, r = 1
• 250 | (-9 * 111 -1) => 250^· = -9 * 111 – 1 => Efectivamente -1000 es múltiplo de 250

Ahora bien, existe un teorema que matiza el anterior:

Existe un entero positivo único a’ menor que m que es un inverso de a (mod m) y cualquier otro inverso de a (mod m) será congruente con a’ (mod m)

Como dijimos en el anterior artículo, el par s y t no es único. La expresión general que nos da todos los coeficientes es:

1 =111(-9 + 250h) + 250(4 – 111h) ∀ h ∈ Z

Para h = 1 tendríamos:

1 = 111*241 + 250*(-107)

Como s = 241 y t = -107 tendremos 111*241 ≡ 1 (mod 250) Por lo tanto es 241 el inverso positivo menor que 250.

Si por un lado tenemos la ecuación de congruencia lineal ax ≡ b (mod m) y esta tiene un a’ ∈ Z tal que a’*a = 1 (mod m) Por otro lado, como cualquier número es congruente consigo mismo módulo m podemos crear la congruencia a’ ≡ a’ (mod m).

Un importante teorema dice:

Sean a, b, c y d enteros y m un entero positivo. Si es a ≡ b (mod m) y c ≡ d (mod m), entonces también es ac ≡ bd (mod m).

Con este teorema, de las dos congruencias anteriores resulta:

ax * a’ ≡ a’ * b (mod m)

Como a’ * a (mod m) = 1 Queda:

1 * x ≡ a’ * b (mod m)

Si existe el inverso modular, es decir, si m y a son primos relativos, o lo que es lo mismo, si mcd(m, a) = 1, todo x congruente con a’ * b (mod m) será solución a la ecuación de congruencia.

Vamos a calcular la solución de 3x ≡ 5 (mod 13):

El programa del artículo anterior, para a y m, es decir, 3 y 13 nos devuelve:

m.c.d. = 1

Bezout s = -4

Bezout t = 1

Como a y m son primos entre si, sin más cálculos podemos ver que el inverso de 3 (mod 13) es 9, pero procedamos como hemos visto. Si el inverso es -4 necesitamos encontrar el positivo, busquemos para ello otro par s y t con h = 1:

1 = 3*(-4 + 13*1) + 13*(1 – 3*1) = 3*9 + 13*(-2)

Por esta vía también obtenemos a’ = 9. Todo x congruente con 9*5 (mod 13) será solución. Como 45 (mod 13) = 6, todos los múltiples de 13^· + 6 serán las soluciones a 3x ≡ 5 (mod 13). Por lo tanto, x ≡ 6 (mod 13) es una congruencia equivalente más simple.

Vamos a calcular la solución de 5x ≡ 2 (mod 6):

El programa nos devuelve:

m.c.d. =  1
Bezout s =  -1
Bezout t =  1

Como a y m son primos entre si, tendremos que el inverso a’ es -1. Busquemos el positivo:

1 = 5 * (-1 + 6*1) + 6*(1 – 5*1) = 5 * 5 + 6 * -4

El inverso positivo menor que m es 5.

5*2 (mod 6), 10 (mod 6), x ≡ 10 (mod 6) Los infinitos x congruentes con 10 módulo 6 serán solución de 5x ≡ 2 (mod 6). Es decir, todos los múltiples 6^· + 4 Por lo tanto, es equivalente x ≡ 4 (mod 6)

Cuando a y m no son primos entre si, es decir mcd(a, m) > 1 y b es un múltiplo del mcd, es decir mcd | b, la congruencia tiene solución. Si queremos entender el proceso para hallar las soluciones y no limitarnos a aplicar fórmulas será necesario introducir los conjuntos de restos y las clases de equivalencia, pero para ello será necesario un nuevo artículo.

El siguiente programa en Python calcula las ecuaciones de congruencia que se han tratado en este artículo.

#! /usr/bin/env python
# -*- coding: utf-8 -*-
# Resuelve ecuaciones de congruencia tipo ax ≡ b (mod m)

import sys
from sys import argv

def extendedEuclideanAlgorithm(old_r, r):
    negative = False
    s, old_t = 0, 0
    old_s, t = 1, 1

    if (r < 0):
        r = abs(r)
        negative = True

    while r > 0:
            q = old_r / r
            #MCD:
            r, old_r = old_r - q * r, r
            #Coeficiente s:
            s, old_s = old_s - q * s, s
            #Coeficiente t:
            t, old_t = old_t - q * t, t

    if negative:
        old_t = old_t * -1
        
    return old_r, old_s, old_t

a = long(argv[1])
b = long(argv[2])
m = long(argv[3])
#Para las soluciones no necesitaremos t pero lo recogemos para evitar el error.
mcd, s, t = extendedEuclideanAlgorithm(a, m)
if mcd == 1:
    inverse = (s * b) % m
    print "x ≡ {0} (mod {1})" . format(inverse, m)
elif b%mcd == 0:
    print "Ver siguiente artículo"
else:
    print "No tiene solución"

Para resolver la ecuación 3x ≡ 5 (mod 13) haríamos:

vic@LESBIAN:~/mates$ ./inversoModulo.py 3 5 13
x ≡ 6 (mod 13)

Editado el 11/03/2018:

Casi un año después de su publicación, observo en Google Analytics que este artículo tiene un porcentaje de rebote muy elevado. Tal vez este sea debido a que la mayoría de visitantes estén buscando simplemente un programa que calcule el mcd de dos números y sus coeficientes de Bezout. Si es tu caso, puedes instalar fácilmente el intérprete de Python 2 en tu ordenador, es muy ligero y existe para todas las plataformas. Como alternativa, dispones de intérpretes en línea (1, 2) donde puedes copiar y pegar el código; después deberás modificarlo ligeramente porque los parámetros no serán argumentos pasados a través de la línea de comandos.

He hecho un breve programa en Python que calcula el máximo común divisor (mcd) de dos números pasados como parámetros y sus coeficientes de Bezout. El teorema de Bezout nos dice que dados dos números a y b, cuyo mcd(a, b) = d existen dos números enteros s y t tales que:

a*s + b*t = d

Estos dos números s y t son los llamados coeficientes de Bezout. Este par s y t no tiene por qué ser único, pueden haber otros s y t que cumplan la igualdad. La identidad de Bezout no es una mera curiosidad matemática sino que tiene muchas aplicaciones: desde calcular el inverso de a módulo m, lo que permite resolver ecuaciones de congruencia lineal, hasta resolver ecuaciones diofánticas.

El máximo común divisor se puede calcular a mano como nos enseñaron en la escuela mediante el algoritmo de Euclides. Los coeficientes de Bezout los podemos calcular a mano mediante el algoritmo extendido de Euclides, pero a la hora de programar es más fácil implementar el siguiente algoritmo explicado en la Wikipedia.

Todos estos valores se calculan mediante la división euclídea y esta impone la condición 0 >= r < |d| Es decir, el resto debe ser mayor o igual a 0 y menor que el valor absoluto del divisor. Como expliqué en un artículo anterior, Python no hace la división euclídea cuando el divisor es negativo, por lo tanto en el código hago una pequeña manipulación al signo del segundo número para obtener los coeficientes de Bezout con los signos correctos.

#! /usr/bin/env python
# -*- coding: utf-8 -*-

import sys
from sys import argv

old_r = long(argv[1])
r = long(argv[2])
negative = False
s, old_t = 0, 0
old_s, t = 1, 1

if r < 0:
    r = abs(r)
    negative = True

while r > 0:
    q = old_r / r
    #MCD:
    r, old_r = old_r - q * r, r
    #Coeficiente s:
    s, old_s = old_s - q * s, s
    #Coeficiente t:
    t, old_t = old_t - q * t, t

if negative:
    old_t = old_t * -1
    
print "m.c.d. = ", old_r
print "Bezout s = ", old_s
print "Bezout t = ", old_t

Ejemplo de su ejecución desde la terminal:

vic@LESBIAN:~/mates$ ./bezoutYmcd.py 23 -4
m.c.d. =  1
Bezout s =  -1
Bezout t =  -6

Si convertimos este programa en una función tendremos una herramienta útil para calcular el inverso de a módulo m, resolver ecuaciones de congruencia lineal y ecuaciones diofánticas.