Evolución de casos de coronavirus en España

Posted on por

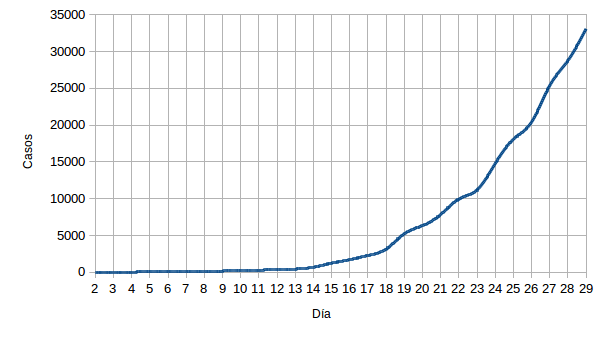
En la anterior entrada estimé el crecimiento de casos en España a partir de un titular de un diario, en el presente se pretende hacer una estimación mejor fundamentada. En todo caso, ni en el anterior ni en el presente artículo estoy haciendo nada más que un pasatiempo, sin mayores pretensiones. Una vez aclarado que para cualquier estudio serio del tema deben consultarse fuentes oficiales, podemos empezar. En primer lugar, vamos a trabajar con los datos que proporciona el Ministerio de Sanidad del Gobierno de España:

Fecha Día Casos Ln(Casos)
24/02/20 1 4 1,3862943611
25/02/20 2 8 2,0794415417
26/02/20 3 14 2,6390573296
27/02/20 4 26 3,258096538
28/02/20 5 45 3,8066624898
29/02/20 6 59 4,0775374439
01/03/20 7 84 4,4308167988
02/03/20 8 125 4,8283137373
03/03/20 9 169 5,1298987149
04/03/20 10 228 5,429345629
05/03/20 11 282 5,6419070709
06/03/20 12 365 5,8998973536
07/03/20 13 430 6,0637852087
08/03/20 14 674 6,5132301109
09/03/20 15 1231 7,1155821262
10/03/20 16 1695 7,4354380198
11/03/20 17 2277 7,7306140661
12/03/20 18 3146 8,0538870836
13/03/20 19 5232 8,5625488931
14/03/20 20 6332 8,753371421
15/03/20 21 7844 8,9675041873
16/03/20 22 9942 9,2045234867
17/03/20 23 11178 9,3217028398
18/03/20 24 14769 9,6002856684
19/03/20 25 18077 9,802395691
20/03/20 26 20410 9,9237802558
21/03/20 27 25374 10,1414803067
22/03/20 28 28768 10,2670189373
23/03/20 29 33089 10,4069561798

Las columnas «Fecha» y «Casos» son los datos oficiales, mientras que las columnas «Día» y «Ln(Casos)» se han añadido para realizar las estimaciones. Desde los medios de comunicación se repite que el crecimiento es exponencial, algo que podemos comprobar que es cierto si hacemos una representación gráfica a partir de los datos de la tabla:

casos coronavirus españa

(1)

Sigue leyendo →

Cómo probar las consultas de manipulación de datos antes de ejecutarlas en MySQL

Posted on por

base de datos mysql

Las instrucciones SQL de manipulación de datos o DML (Data Manipulation Language) pueden producir una grave pérdida o alteración de los datos. Un descuido en la sintaxis al escribir una orden UPDATE, por ejemplo, o cualquier otro «detalle» que pase desapercibido en ese momento pueden tener unas consecuencias completamente indeseadas para los valiosos datos. Para evitar caer en esa situación, existen dos posibilidades que no son mutuamente excluyentes. La primera, la más evidente, usar la instrucción por excelencia del DQL (Data Query Language):

SELECT

En un caso hipotético, se desea concatenar los campos del piso (adfloor) y el número (adnumber) a la dirección (address) como paso previo a la eliminación de estos. Un SELECT que adelante los resultados del UPDATE sería:

SELECT address, adnumber, adfloor,
concat(coalesce(address, ''), ' ', coalesce(adnumber, ''), ' ', coalesce(adfloor, '')) AS address_concat
FROM table;

Si los resultados son los esperados, puede lanzarse el UPDATE:

UPDATE table
SET address = concat(coalesce(address, ''), ' ', coalesce(adnumber, ''), ' ', coalesce(adfloor, ''));

La segunda, es mediante TCL (Transaction Control Language):

Transacciones

Sigue leyendo →

Aritmética modular para entender el complemento a 2

Posted on por

Los ordenadores codifican internamente los números en binario. Los enteros pueden representarse mediante dos sistemas de representación: el complemento a 2 (Ca2 para abreviar) y el de signo y magnitud. Para los humanos es más amigable el segundo de ellos, pues consiste en reservar el primer bit para indicar si se trata de un positivo o negativo (0 o 1) y el resto es el valor absoluto del número. No obstante, en la mayoría de ordenadores hace ya bastantes años que se emplea el primero, pues goza de dos ventajas: un mayor rango de representación posible al mismo número de bits – pues tiene una única representación para el 0 – y mayor velocidad de ejecución por parte del microprocesador de las operaciones de resta y suma. En el presente artículo, se explicará cómo funciona el complemento a dos, porqué permite realizar las operaciones aritméticas más rápidamente y porqué su resultado debe interpretarse.

En primer lugar, para entender cómo funciona, el lector debe conocer lo básico de la aritmética modular y las clases de equivalencia. En caso de que lo desconozca o bien necesite refrescarlo, al inicio de este artículo se introducen.

Los procesadores representan los números enteros en 8, 16, 32 o 64 bits dependiendo del microprocesador. Para simplificar los ejemplos inicialmente se emplearán 3 bits, que permiten representar 23 = 8 dígitos, es decir, los números comprendidos entre el 0 y el 7. Si se excede el rango, debido a la aritmética modular se sigue obteniendo un resultado, por ejemplo:

  • 2 + 4 = 6 No sobrepasa el límite, el resultado es el esperado.
  • 4 * 2 = 0, pues 0 ≡ 8 (mod 8)
  • 4 + 5 = 1, pues 1 ≡ 9 (mod 8)

Sigue leyendo →

Debug en la barra de Symfony desde Twig

Posted on por

Este es un pequeño truco para que el volcado mediante dump() de una variable en Twig no aparezca en medio del HTML sino que lo haga en la barra de Symfony, tal y como sucede cuando el volcado se hace desde el código PHP (por ejemplo en un controlador, entidad, etc.) Curiosamente, esto no aparece en la documentación de Twig, de ahí el nombre de «truco».

Los ejemplos de uso que aparecen:

{{ dump(app.request.locale) }}

Pueden llegar a provocar un molesto resultado:

dump en el html

En cambio, si lo tratamos como una instrucción más mediante {% en vez de {{, el resultado se mostrará en el profiler de Symfony:

{% dump(app.request.locale) %}


Lo cual nos facilitará la vida en algunas circunstancias.

Puntuación de 100 en Google PageSpeed Insights

Posted on por

La velocidad de carga de una página no tan solo influye en la usabilidad de la misma, sino que también es una de las variables en el algoritmo de Google para decir el posicionamiento de la web en los resultados de búsqueda. Para la medición del tiempo de descarga, los de Mountain View ponen a disposición de los desarrolladores la herramienta PageSpeed Insights.

Recientemente han cambiado la aplicación y resulta factible obtener la puntuación máxima de 100. Antes simplemente era imposible para cualquier web práctica, a modo de ejemplo: la mera inclusión del fichero Javascript para Google Analytics ya restaba, haciendo imposibles los cien puntos, pues al tratarse de un recurso remoto, no podemos alterar la fecha de caducidad de su caché.

Un proyecto realizado hace dos años, del que me encargué tanto de la programación como de los aspectos técnicos, conseguía puntuaciones muy cercanas a 100: 97, 98… Con el nuevo sistema alcanza la puntuación máxima, y lo hace también en la sección donde es más difícil, por ser la que más contenidos carga: la página principal, como puede observase en la captura de pantalla.

Sigue leyendo →