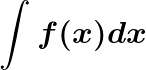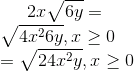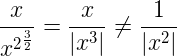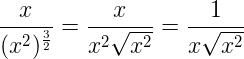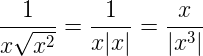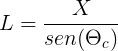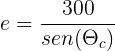La Inteligencia Artificial como último legado del ser humano

Posted on agosto 12, 2018 por Víctor Iglesias Castán

En este artículo divago, sin pretensión, sobre diferentes temas que me han interesado a lo largo de la vida: la finitud de la misma (tanto la individual como la del conjunto de los seres de este planeta), las distancias insalvables del espacio y su hostilidad a la vida, el sentido de esta… y la informática. Desde luego, el ser humano es algo más que inteligencia, así como para la vida la inteligencia es sólo una herramienta más, como las garras y los dientes o la capacidad de ver de noche, pero a largo plazo, tal vez sea lo único que podamos hacer perdurar.

El planeta tierra no podrá sustentar indefinidamente la vida, especialmente las formas de vida más complejas, como la nuestra, que son también las más delicadas: tenemos mucha menos resistencia que, por ejemplo, las cucarachas, y estás a su vez se quedan cortas frente a determinadas bacterias y virus, algunos capaces de permanecer latentes durante siglos antes de volver a despertar. Ahora mismo, nuestra civilización se enfrenta a dos grandes problemas:

La crisis energética.
El cambio climático.

Sigue leyendo →

Redimensión de imágenes proporcionalmente en PHP

Posted on julio 21, 2018 por Víctor Iglesias Castán

Una necesidad que surge en todas las webs cuyos contenidos son introducidos por un usuario (o varios) a través de un gestor de contenidos, es adaptar las imágenes que estos suben al diseño de la misma para que no se deforme. Además, las proporciones de una imagen en una sección pueden ser diferentes a cómo se muestra en otra; un caso típico es usar una proporción para un listado y otra para la ficha de cada elemento, por ejemplo las noticias, los productos, etc.

Para resolver este problema sirve el conjunto de clases PHP que presentó en este artículo. Este software, a partir de una imagen original, creará una copia por cada tamaño que necesitemos. El proyecto completo puede verse en Github y el objetivo del presente artículo es explicar cómo funciona. En primer lugar, instanciamos la clase:

$objResize = Signia_ImageResize_Factory::getInstanceOf($srcFile, $destFile, $newSize);

Donde:

$srcFile es el path hacia la imagen que ha subido el usuario.
$desFile es el path de la imagen de destino.
$newSize es el tamaño deseado.

A partir de un array con los tamaños deseados podemos crear un bucle por cada uno de ellos ($newSize). Los índices widthMax y heigthMax hacen referencia al tamaño máximo permitido, mientras que width y height pueden entenderse como widthMin y heightMin. Veamos un ejemplo:

$imageType = [
  'slide' => ['width' => 1000, 'widthMax' => 1000, 'height' => 400, 'heightMax' => 400, 'background' => '000000'],
  'r2_34' => ['width' => 468, 'widthMax' => 2340, 'height' => 200, 'heightMax' => 1000],
  'r2_7'  => ['width' => 1080, 'widthMax' => 2700, 'height' => 400, 'heightMax' => 1000],
  'r1_6'  => ['width' => 459, 'widthMax' => 1000, 'height' => 287, 'heightMax' => 625],
  'r1'    => ['width' => 266, 'widthMax' => 266, 'height' => 177, 'heightMax' => 177]
];

En Factory.php podemos ver la clase Signia_ImageResize_Factory:

class Signia_ImageResize_Factory
{
	static public function getInstanceOf($srcImageName, $destImageName, $newSize)
	{
		$aux       = explode(".", $destImageName);
		$extension = end($aux);
		if (preg_match("/jpg|JPG|jpeg|JPEG/", $extension)) {
			$extension = "jpeg";
		}
		$imageResizer = "Signia_ImageResize_" . ucfirst($extension);

		return new $imageResizer($srcImageName, $destImageName, $newSize);
	}
}

Sigue leyendo →

Generalización de los espacios vectoriales

Posted on junio 30, 2018 por Víctor Iglesias Castán

El conjunto de los vectores libres del plano ℝ² o del espacio ℝ³, es sólo uno del los muchos objetos matemáticos que pueden formar un espacio vectorial. Este concepto se puede abstraer para englobar no sólo vectores sino también otros objetos como polinomios, funciones o conjuntos de números. En este artículo expondré cómo se realiza esta generalización, en primer lugar para tenerlo yo claro, y en segundo lugar, para ayudar a otros; aunque para este segundo caso debo aclarar al lector que yo no soy matemático y por lo tanto sugiero contrastar lo que aquí expongo con fuentes acreditadas.

En color amarillo está representado el vector (3, 2, 1) y en violeta el (-1, 0, 2).

Los vectores, tanto en el plano como en el espacio, tienen dirección, sentido y módulo. Si lo pensamos, la abstracción del concepto ya empieza simplemente si nos desplazamos a ℝ⁴ , pues, ¿cómo representar en este espacio dichos valores? No podemos, resulta que fuera del plano y el espacio tridimensional donde nos introdujeron los vectores en el Bachillerato, el vector ya es una abstracción. La siguiente definición y propiedades nos permitirá ir más allá de ℝ³, e incluso de los vectores, con rigurosidad:

Sigue leyendo →

Funciones de orden superior

Posted on junio 27, 2018 por Víctor Iglesias Castán

Tanto en matemáticas como en informática, las funciones de orden superior son aquellas que cumplen, al menos, una de estas condiciones:

Esperan como argumento/s una o más funciones.
Devuelven una función como resultado.

Ejemplos en matemáticas son la derivada y la antiderivada o función primitiva.

El operador diferencial es una función de orden superior

La antiderivada de una función f es una función F tal que F’ = f

En informática son la esencia de los lenguajes funcionales, pero también aparecen en lenguajes de otros paradigmas. Este es un ejemplo en el lenguaje Scheme en el que la función (f x) recibe un argumento y devuelve una función:

(define (f x)
  (lambda (y) (+ x y)))
(display ((f 3) 7))

Puede ejecutarse aquí para ver el resultado.

Cuando nació Javascript, a algunos programadores les pareció un lenguaje orientado a objetos fallido¹, sobretodo porque, por razones comerciales, se le puso un nombre que lo asocia con Java. Desconozco si su creador estuvo muy de acuerdo con ese nombre pues, tal y como se diseño este lenguaje, da bastante juego a la programación funcional. En el siguiente ejemplo, el método filter() es una función de orden superior, pues espera recibir una función como parámetro:

function isPrime(x){
  if (x === 2) {
     return true;
  }
  let test = x%2 !== 0;
  let i = 3;
  stop = Math.floor(Math.sqrt(x)); // Raíz entera de x
  while (test && i <= stop) {
	  test = x%i !== 0;
	  i = i + 2;
  }
  return test;
}

const numbers = [47, 139, 137, 213, 2, 3, 45, 1515];
const primeNumbers = numbers.filter(isPrime);
console.log(primeNumbers);

Lo que este programa hace es filtrar la formación de números naturales «numbers«, dejando sólo los que sean primos en «primeNumbers«. Cada elemento de «numbers» será evaluado por la función «isPrime» mediante la criba de Eratóstenes. El lector puede ejecutarlo accediendo a la consola del navegador pulsando F12 y modificar el valor de «numbers» con los números (o el número) que quiera saber si son primos o no.

Este tipo de funciones están en prácticamente todos los lenguajes modernos, incluso en los que no se tuvo en cuenta el paradigma funcional en el momento de su creación. Es el caso de PHP, donde podemos encontrar una gran cantidad de funciones que esperan otra función, como es el caso de, por ejemplo, preg_replace_callback()²:

$capitalice = function($coincidencia) {
    return strtoupper($coincidencia[1]);
};

echo preg_replace_callback('~-([a-z])~', $capitalice, 'hola-mundo');

Además de usar las implementadas en funciones y métodos propios del lenguaje, también podemos crear las nuestras, de forma parecida a un lenguaje completamente funcional. En Javascript, la Wikipedia nos ofrece el siguiente ejemplo:

const twice = (f, v) => f(f(v));
const add3 = v => v + 3;

console.log(twice(add3, 7));

Lo mismo es posible en PHP:

$twice = function($f, $v) {
    return $f($f($v));
};

$f = function($v) {
    return $v + 3;
};

echo($twice($f, 7));

La programación funcional pretende tratar la programación como la evaluación de funciones matemáticas, paradigma muy diferente a la programación imperativa, basada en estados y en instrucciones que lo cambian. Tal vez las características funcionales que tienen algunos lenguajes puedan ayudarnos a introducirnos en un paradigma, el funcional, que nos exige una forma muy distinta de enfocar los problemas.

¹ Todavía hoy en día, y a pesar de los cambios que ha sufrido en los últimos ECMA, sigue despertando las críticas de los programadores que, debido a su nombre, esperan que se comporte como un lenguaje completamente orientado a objetos, como Java, y se dan de bruces contra la realidad.

² El parámetro que recibe la función contenida en $capitalize son las coincidencias que encuentre la expresión regular.

Cómo intercambiar el valor de dos variables enteras sin una intermedia

Posted on junio 23, 2018 por Víctor Iglesias Castán

Cómo intercambiar el valor de dos variables enteras sin una intermedia es, en mi opinión, una mera curiosidad. Ahora bien, parece ser que en algunas entrevistas de trabajo aparece esta pregunta. Cuando se me ha pedido colaborar en el proceso de selección de un futuro compañero, no se me ha ocurrido incluir semejante pregunta en la prueba, pues no creo que esta sirva para apreciar la calidad de un programador. No obstante, si el presente artículo, además de presentar una anécdota, le sirve a alguien a superar una prueba, será un plus.

A continuación, voy a exponer dos métodos que, al usar Javascript para su implementación, el lector podrá ejecutarlos fácilmente presionando F12 para acceder a la consola. Sigue leyendo →

Cuando las matemáticas se explican mal

Posted on junio 20, 2018 por Víctor Iglesias Castán

En la EGB nos podrían haber explicado mejor las matemáticas, me di cuenta de esto años después, en Bachillerato, y a las malas. Si no es tu caso, me alegro por ti; en el nuestro tuvimos profesores que no tenían claro lo que explicaban, no se trataba de saber mucho (es sólo la EGB) sino de tenerlo muy claro. En mi opinión, en matemáticas es preferible avanzar poco pero con firmeza a avanzar mucho sin solidificar las bases, lo que conduce más pronto que tarde al desmoronamiento de lo que creíamos saber.

A continuación, expondré cómo me parece que hubiera sido mejor que explicaran algunos aspectos. Si eres profesor, espero que te pueda servir mi opinión (puedes dejarme la tuya en los comentarios); si eres alumno de la educación obligatoria, tal vez esto puedo ayudarte a clarificar algunos conceptos.

Los miembros de una ecuación no «pasan» al otro lado

Recuerdo que el profesor usaba expresiones como:

x pasa a dividir (o a multiplicar) al otro lado.
Tal número pasa a restar (o a sumar) al otro lado.

Como ejemplo de los errores a los que puede conducir pensar así, veamos la ecuación de la división entera, donde D es el dividendo, d el divisor, q el cociente y r, r≥0, el residuo:

D = d*q + r

Si pensamos que D «pasa a dividir al otro lado», como el lado izquierdo de la igualdad queda vacío, podemos creer que esto es correcto:

0 = (d*q + r) / D

Si nos hubieran enseñado que, como ambos lados de la ecuación son iguales, la igualdad se mantendrá si operamos igual en ambos lados, pensaremos que vamos a dividir a ambos lados por D, con lo que llegaremos a una igualdad correcta:

D/D = (d*q + r) / D → 1 = (d*q + r) / D

Segmentar la resolución de una ecuación

Otra zancadilla en nuestro aprendizaje nos la daba un profesor que usaba el punto y coma «;» para separar cada paso que ejecutaba para resolver la ecuación. Arrastré la coletilla hasta que en el Bachillerato, un compañero me preguntó por qué usaba un punto y coma en vez del signo igual. Tal vez sería más pedagógico usar el símbolo «implica que»:

x² -9 = 0 ; x² = 9 ; x = √3; x = ±3

x² -9 = 0 ⇒ x² = 9 ⇒ x = √3 ⇒ x = ±3

Lo que implica la igualdad

Deberían habernos dejado bien claro, incluso diría que machacado, que el hecho de que los dos lados de la ecuación sean iguales implica que seguirán siéndolo si se realiza la misma operación en ambos lados: elevar al cuadrado, al cubo, raíz cuadrada a ambos lados, etc. Cuando llega el momento, no está de más explicar que operaciones como las raíces pueden tener la limitación x ≥ 0 cuando operamos ecuaciones que las contienen, por ejemplo:

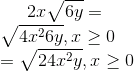
Estas condiciones son frecuentes en matemáticas: aparecen en los logaritmos y, pasada la educación obligatoria, vuelven a aparecer en el cálculo de límites, en las integrales, etc.

Potencia con exponente

En matemáticas se tiende a obviar los paréntesis que no son imprescindibles, esto nos puede inducir a creer que la siguiente igualdad es cierta, cuando no lo es:

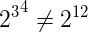En este caso, por la prioridad de los operadores, primero debe calcularse 3⁴, 81, para finalmente operar 2⁸¹. En cambio, mediante los paréntesis podemos indicar que la base no es 2 sino 2³, es decir, la potencia de una potencia:

Simplificaciones incorrectas

En el trabajo de una expresión matemática nunca puede irse en «piloto automático» sino que hay que tener muy claro en cada paso lo que se está haciendo. Esto es fundamental en el aprendizaje de las matemáticas.

Consecuencia del ejemplo anterior con la raíz, la siguiente simplificación, en algunas circunstancias, es falsa:

√x² ≠ x

La correcta es:

√x²= |x|

Cuando nos dan la fórmula de la ecuación de segundo grado, aparece el ± acompañando la raíz del radicando. Pues bien, cuando unas clases más adelante se explica que un elemento al cuadrado dentro de una raíz se simplifica, se debería dejar muy claro que, por convención, √x hace referencia a la solución positiva, mientras que -√x se refiere a la negativa. Por ejemplo:

√9 = 3

-√9 = -3

En el caso del cuadrado dentro de la raíz, sería:

√3² = 3

No obstante, en el caso de la raíz positiva, se produce una ambigüedad que se solventa mediante el empleo del valor absoluto. Esta ambigüedad surge porque se obtienen resultados diferentes dependiendo de si se elimina primero la raíz o se calcula primero la potencia:

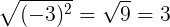
Gracias al valor absoluto, se aclara que sólo se hace referencia la solución positiva, √ en vez de -√. Como anécdota, decir que obviar esto conduce a una demostración según la cual 2 + 2 = 5.

Esta otra trampa de simplificación es algo más sutil, partiendo del hecho que:

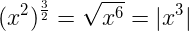Es decir, el resultado no es x³, podemos caer en el siguiente error:

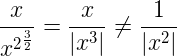La no igualdad sólo se convertiría en igualdad para los casos x > 0. Ahora bien, si sí o sí es necesario sacar la x del numerador, esta simplificación también es correcta:

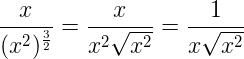Y, efectivamente:

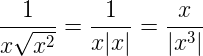
Por si habían dudas

La proporcionalidad

Acerca de las fracciones nos enseñaron prácticamente todo, pero viéndolo desde la distancia, me parece que se pasó a la ligera por el hecho de que el cociente entre dos magnitudes expresa cuánto de la magnitud del numerador corresponde a cada unidad de la magnitud del denominador. Después, en el Bachillerato, esto aparece de forma masiva en asignaturas como Química y Física:

F/m: La aceleración es la fuerza que actúa por unidad de masa.
F/q: La intensidad del campo eléctrico es la fuerza que actúa por unidad de carga eléctrica.
d = m/V: La densidad es la masa de un objeto por unidad de volumen.

En el cotidiano acto de la compra tenían nuestros profesores un buen ejemplo, si por ejemplo un cartel anuncia que la malla de 6 Kg de naranjas cuesta 3’84€ y queremos saber cuánto cuesta el kilogramo, tendremos que poner el precio en el numerador y el peso en el denominador, pues deseamos conocer el precio en función del peso.

Aunque el ejemplo de la compra pueda parecer muy básico, el mismo concepto, la proporcionalidad, permite hallar la solución a problemas aparentemente más complejos, como el siguiente que nos servirá a modo de ejemplo. Tenemos un tramo de fibra óptica de 300 metros por el que se desplaza un haz de luz (línea negra), «rebotando» por reflexión total interna.

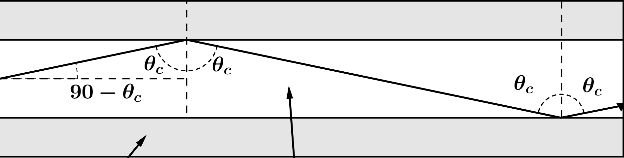
Esquema del tramo de fibra óptica

Si sólo sabemos el valor de ϴ_c como la luz no se desplaza en línea recta sino en zigzag, aparentemente no podemos calcular la distancia real que recorre la luz, pero gracias a la proporcionalidad directa y algo de trigonometría podemos encontrar solución.

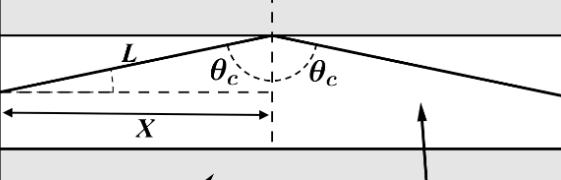
El seno de un ángulo es el cateto opuesto entre la hipotenusa

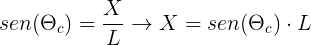Vemos que existe una proporcionalidad directa entre X y L, pues sen(ϴ_c) es una constante. Es decir, si en 300 metros caben n segmentos X, habrá el mismo número de segmentos L, n ∈ ℝ⁺. Como: 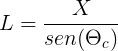Si llamamos e a la distancia real recorrida por luz, sabemos que la siguiente igualdad, que nos permite calcular la distancia realmente recorrida en zigzag, es cierta:

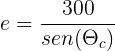En definitiva, creo que una mayor dedicación y rigurosidad en la exposición de los conceptos básicos nos hubiera ayudado a aposentar los cimientos de las matemáticas; una asignatura difícil, incluso para enseñarla.