Una serie de artículos acerca de la exponenciación con números complejos, que di por finalizada en su tercera entrega, y a los que el lector puede recurrir si no entiende algo de lo que en el presente artículo se explica, voy a ampliarla para el curioso caso de iⁱ, y digo curioso pues el resultado es un número real.

Vimos que la generalización de la exponenciación, a^b, sean a y b reales¹ o complejos, es:

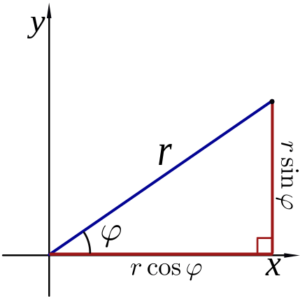
En el presente caso, a = i, y si bien el logaritmo complejo existe, aplicando la fórmula de Euler, podremos obtener la forma exponencial para calcular fácilmente iⁱ. En primer lugar, vamos a expresar i en forma polar para obtener dos datos que necesitaremos: el módulo y el argumento. El módulo, obviamente, será 1 y el argumento será π/2 radianes, pues i forma un ángulo recto con la parte real o eje de las ordenadas:

Por lo tanto, i = 1_π/2 en polar, mientras que en binómica es (0 +1i). De esta última, gracias a que conocemos tanto el módulo como el argumento, podemos pasar a la trigonométrica:

Expresión que se deduce por trigonometría:

Gracias a la fórmula de Euler donde x es el argumento:

Podemos convertir, finalmente, la unidad imaginaria a la forma exponencial:

Por lo que:

Como i = √-1:

Y ya hemos calculado iⁱ.

En rojo el número i y en azul r = iⁱ en el plano complejo.

Si a ∈ ℝ, a > 0